Perceptron and convergence theorem

Motivation

lion

There are lion and tiger. How can we discriminate Lion and Tiger? Someone said that:

  • Tiger has stripe on its head
  • Lion has mane on its head

This information such as striped pattern and the mane is called features in the machine learning.

feature

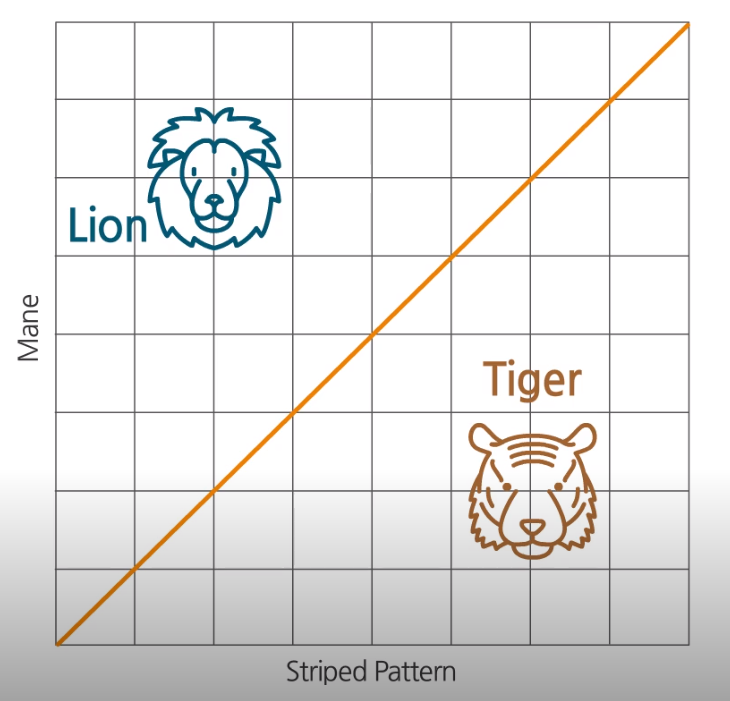
How can we make Intelligence to classify Lion and Tiger automatically? If we can map each creature into feature space, we can divide them with a line and classify as lion for the data above the line, and classify as tiger for the data below the line. At this case, the line regards as an intelligence distinguishing lion and tiger.

To generalize this problem, we have 2 types of label (Class1 and Class2). And each data has 2-dimension coordinates.

x=[x1x2]Tx = [x_1 \quad x_2]^T

Then, we can define the line $f(x) = x_2 - x_1$. If $f(x) > 0$, it must be Class1, and if $f(x) < 0$, then it must be Class2. Our goal is to introduce the algorithm for finding the function from the data.

Hyperplane

The line in the previous example is called as a hyperplane in a high dimensional space. The hyperplane can be defined in the arbitrary D-dimensional space and should separate the defined space into two disjoint spaces.

In mathematical form, it relates to normal vector $W$ and bias $b$. Especially, the hyperplane can be represented by the inner product between the normal vector and the data points in the input space, then adding bias.

WTX+b=0 where W=[w1…wn]T,X=[x1…xn]T,b∈RW^T X + b = 0 \\ \text{ where } W = [w_1 \dots w_n]^T, X = [x_1 \dots x_n]^T, b \in \mathbb{R}

For example, consider a 2-dimension example.

W=[−11]T,b=0W = [-1 \quad 1]^T, \quad b = 0

In this case, hyperplane $f(X)$ is:

f(X)=[1−1][x1x2]=−x1+x2=0f(X) = \begin{bmatrix} 1 -1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = -x_1 + x_2 = 0

And we can call $W$ as normal vector of the hyperplane (unnormalized)

feature

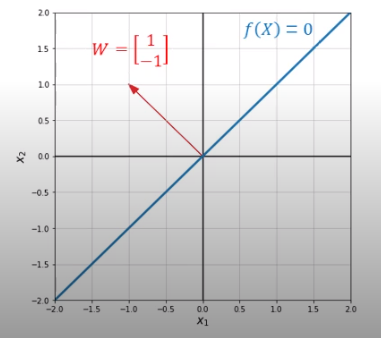
The red line is normal vector, and blue line is hyperplane. As you can see this, the normal vector is orthogonal ($90^\circ$) to any vector or data point lying on the hyperplane. As a result, hyperplane is defined by an normal vector and bias.

feature2

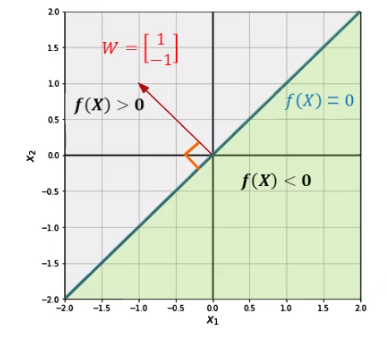
We can color the region based on the sign of the output of the hyperplane. In the previous example, the hyperplane itself has 0. So it is also called decision boundary

Perceptron

So we found out that to handle binary classification, we need to find hyperplane from the given data. How can we do that?

One answer is Perceptron. Perceptron is an algorithm for supervised learning of binary classification problem. It requires the training dataset that includes Input $X$ and Corresponding label $y$.

perceptron

From the figure, we can guess the prediction process of the perceptron briefly. The sign of sum of all value becomes the predicted label. In details, the sum of value is decomposed by inner product between the weight of the perceptron and the input vector, and adding bias.

This process is similar with the definition of the hyperplane. So we can use this algorithm to find the hyperplane.

For example,

perceptron2

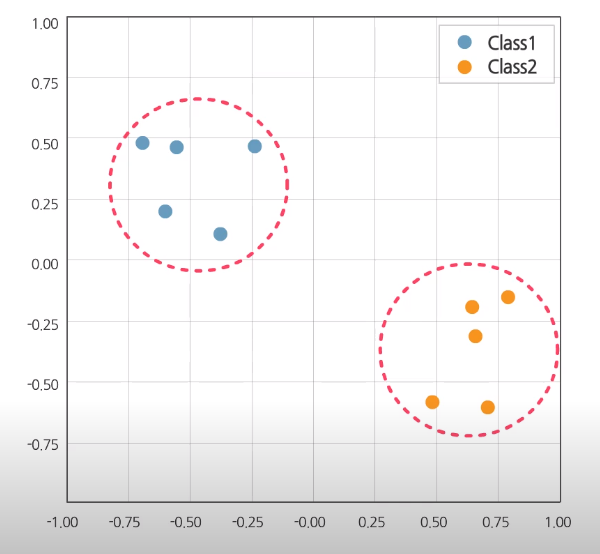
Given training dataset, (X1,y1),(X2,y2),…,(X10,y10)where Xi=[x1x2]T,yi∈{−1,1}(X_1, y_1), (X_2, y_2), \dots , (X_{10}, y_{10}) \\ \text{where } \quad X_i = [x_1 \quad x_2]^T, y_i \in \{-1, 1\}

Class 1 has label 1 and Class 2 has label -1. For ease of expression, we uses homogeneous coordinate representation in $X$

Xi=[x1x2]→Xi=[x1x21]X_i = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \rightarrow X_i = \begin{bmatrix} x_1 \\ x_2 \\ 1 \end{bmatrix} W=[w1w2b]TW = \begin{bmatrix} w_1 & w_2 & b\end{bmatrix}^T

From this, we can define the hyperplane.

f(X)=WTX=0f(X) = W^T X = 0

To use perceptron,

  • Initialize the normal vector and bias
  • For $t = 1 \dots T$ (The number of iteration)

Note: $\text{sign}(x) = \begin{cases} -1 & \quad x > 0 \ 0 & \quad x = 0 \ 1 & \quad x > 0 \end{cases}$

  1. $f(X_n) = \text{sign}(W^T X_n)$
  2. If $y_n \neq f(X_n)$, then update $W = W + y_n x_n$ else, leave $W$ unchanged.

update

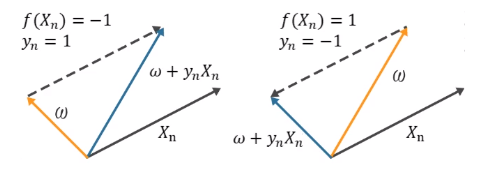
Convergence for the perceptron

Anyway, The question remains that “Does the perceptron algorithm will converge or not?” And, the answer is YES. If the data is linearly separable, its algorithm converges.

There are theorems related on the convergence for the perceptron:

  • Number of update $k$ is bounded in the perceptron algorithm with 2 assumptions.
  1. Assume that there exists some weight vector $W^$ such that $\Vert W^ \Vert = 1$, and some $\gamma > 0$ such that for all $n = 1 \dots N$
ynxnTW∗≥γy_n x_n^T W^* \geq \gamma

Where $\Vert \chi \Vert$ is 2-norm of $x$ (i.e. $\Vert x \Vert = \sqrt{\sum_i x_i^2}$)

  1. Assume in addition that for all $n$,
∥xn∥≤R\Vert x_n \Vert \leq R

From these assumption, the perceptron algorithm have the number of update $K$ is bounded.

k≤R2γ2k \leq \frac{R^2}{\gamma^2}
  • At first, define $W_k$ to be the weight bector when the algorithm makes its $K$th update.
  • Suppose the weight vector is initialized zero vector at the first state ($W_1 = 0$)
  • Next, assuming the weight vector at $K$th update on example $n$, we have,
Wk+1TW∗=(Wk+ynxn)TW∗; by the definition of the perceptron updates=WkTW∗+ynxnTW∗≥WkTW∗+γ;Assumption from theorem (ynxnTW∗≥γ)\begin{aligned} W_{k+1}^T W^* &= (W_k + y_n x_n)^T W^* \qquad \text{; by the definition of the perceptron updates} \\ &= W_k^T W^* + y_n x_n^T W^* \\ &\geq W_k^T W^* + \gamma \qquad \qquad \text{;Assumption from theorem } (y_n x_n^T W^* \geq \gamma )\end{aligned}
  • It follows by induction on $K$ (recall that $\Vert W_1 \Vert = 0$)
Wk+1TW∗≥WkTW∗+γ≥Wk−1TW∗+2γ≥⋯≥kγW_{k+1}^T W^* \geq W_k^T W^* + \gamma \geq W_{k-1}^T W^* + 2 \gamma \geq \cdots \geq k \gamma

  • In addition, because $\Vert W_{k+1} \Vert \dot \Vert W^* \Vert \geq W_{k+1}^T W^*$ (from definition of inner product) and $\Vert W_1 \Vert = 0$, we have $\Vert W_{k+1} \geq k \gamma \Vert$ (This is the lower bound of $\Vert W_{k+1} \Vert$)

  • In the second part of the proof, we will derive an upper bound of $\Vert W_{k+1} \Vert$

∥Wk+1∥2=∥Wk+ynxn∥2=∥Wk∥2+yn∥xn∥2+2ynxnTWk≤∥Wk∥2+R2;Assumption from theorem (∥xn∥≤R);ynxnTWk≤0because the update of perceptron occurs when yn≠sign(xnTWk)\begin{aligned} \Vert W_{k+1} \Vert^2 &= \Vert W_k + y_n x_n \Vert^2 \\ &= \Vert W_k \Vert^2 + y_n \Vert x_n \Vert^2 + 2 y_n x_n^T W_k \\ &\leq \Vert W_k \Vert^2 + R^2 \qquad \text{;Assumption from theorem ($\Vert x_n \Vert \leq R$)} \\ & \qquad \qquad \qquad \qquad \quad \text{;} y_n x_n^T W_k \leq 0 \quad \text{because the update of perceptron occurs when } y_n \neq \text{sign}(x_n^T W_k) \end{aligned}
  • It follows by induction of $k$ (recall that $\Vert W_1 \Vert^2 = 0$)

∥Wk+1∥2≤kR2\Vert W_{k+1} \Vert^2 \leq k R^2 And this is the upper bound of $\Vert W_{k+1} \Vert^2$

Combining the lower bound and upper bound

k2γ2≤∥Wk+1∥2≤kR2k^2 \gamma^2 \leq \Vert W_{k+1} \Vert^2 \leq k R^2

Then, we can get the upper bound for the number of update $k$

k≤R2γ2(The lower bound of ∥Wk+1∥)k \leq \frac{R^2}{\gamma^2} \qquad (\text{The lower bound of } \Vert W_{k+1} \Vert)

As you can see, the boundary is existed in some range. So we can find out that perceptron algorithm has finite update in the training process.

One hyperplane separates the space into 2 half-space. But if the data is not linearly separable, althought the task is binary classification, one hyperplane cannot discriminate labels. In this case, more perceptrons are required to get better result. More effective way to handle is to add the depth(meaning a set of perceptrons) with non-linear function (also known as activation function) We call it Multi Layer Perceptron (MLP) or neural network. If you want the visualization of neural network, check out the following links:

Summary

In this post, it introduced the perceptron algorithm which trains the hyperplane, and tried to look the update rule in the perceptron. Also, we prove the theorem related to convergence for the perceptron.