Maximum Margin Principle and Soft Margin Hard Margin

• Maximum Margin Principle and Soft Margin Hard Margin
  • Linear separable problem
  • Linear non-separable problem
  • Summary

Maximum Margin Principle and Soft Margin Hard Margin

Linear separable problem

Depending on the distribution in the data, it can choose the different learning method to find the best linear hypothesis. And it will also determin whether the problem is linearly separable or not.

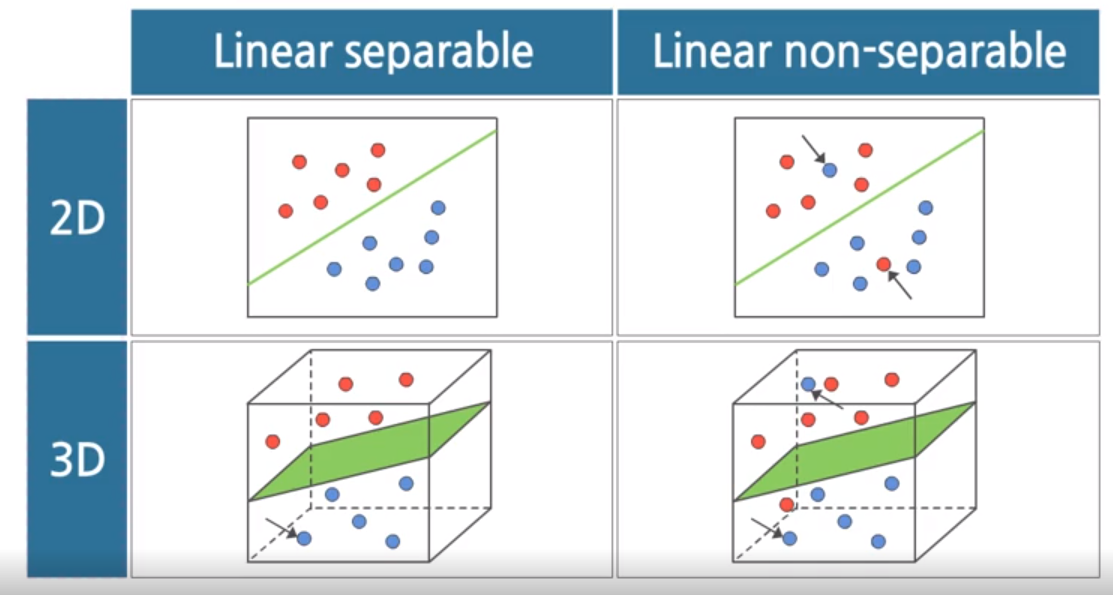
If the dataset is linearly separable, One hyperplane can perfectly classify the label using itself. But if it is not, no linear hyperplane can completely classify two dataset.

In case of linearly separable dataset, there are many candidates to choose hyperplane. But which one is the best?

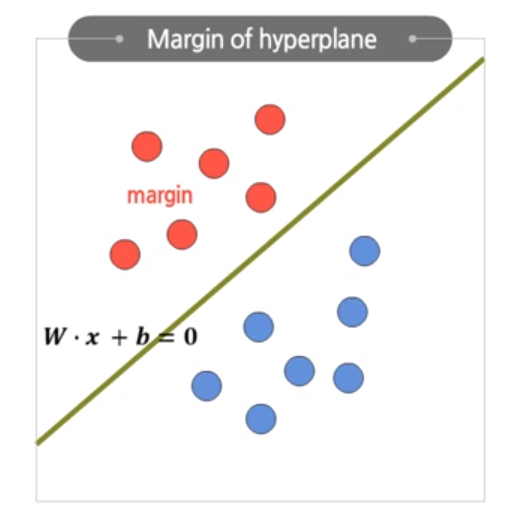
One of the common criteria to choose the best is margin. The margin is an important criteria to select a suitable hyperplane. Margin is defined as the geometric distance from the separating hyperplane to the nearest data points.

If we get the hyperplane $H$ from the previous post,

$$H = \{ x \rightarrow \text{sign}(\mathrm{w} \cdot x + b) \vert \mathrm{w} \in \mathbb{R}^N, b \in \mathbb{R} \}$$

We can define the margin $\rho$ using the distance between the hyperplane and the point,

$$\rho = \min_{i \in [1, m]} \frac{\vert \mathrm{w} \cdot x_i + b \vert}{\Vert \mathrm{w} \Vert}$$

At this time, the data points closest to the hyperplane is called the support vector. If we assume that there are two virtual hyperplanes passing the support vector, Margin can be obtained like this:

$$\rho = \max_{\mathrm{w}, b: y_i (\mathrm{w} \cdot x_i + b) \geq 0} \min_{i \in [1, m]} \frac{\vert \mathrm{w} \cdot x_i + b \vert}{\Vert \mathrm{w} \Vert}$$

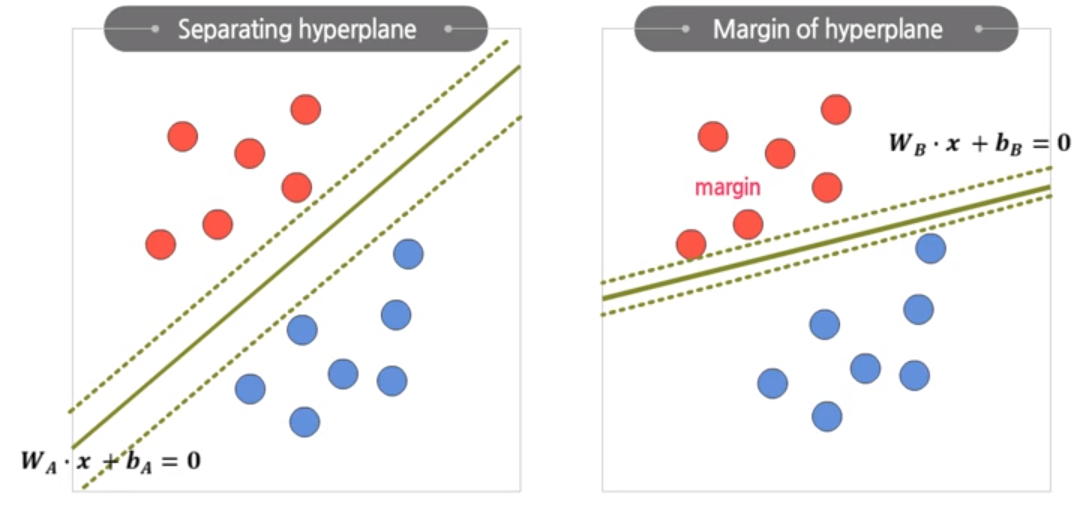
So how can we choose the best hyperplane with this margin? Intuitively, hyperplane with largest margin is selected. In order to get this, few tricks can be appied to simplify the problem.

At first, we can simplify the representation of margin by handling the range of $\mathrm{w}$ and $b$,

$$\begin{aligned} \rho &= \max_{\mathrm{w}, b: (\mathrm{w} \cdot x_i + b) \geq 0} \min_{i \in [1, m]} \frac{\vert \mathrm{w} \cdot x_i + b \vert}{\Vert \mathrm{w} \Vert} \\ &= \max_{\substack{\mathrm{w}, b: (\mathrm{w} \cdot x_i + b) \geq 0 \\ \min_{i \in [1, m]} \vert \mathrm{w} \cdot x_i + b \vert = 1}} \min_{i \in [1, m]} \frac{\vert \mathrm{w} \cdot x_i + b \vert}{\Vert \mathrm{w} \Vert} \quad \text{(scale-invariance)} \end{aligned}$$

We just consider the specific condition, that is,

$$\min_{i \in [1, m]} \vert \mathrm{w} \cdot x_i + b \vert = 1$$

So we can simplify the Margin at that condition, then remove the range handling.

$$\begin{aligned} \rho &= \max_{\substack{\mathrm{w}, b: (\mathrm{w} \cdot x_i + b) \geq 0 \\ \min_{i \in [1, m]} \vert \mathrm{w} \cdot x_i + b \vert = 1}} \frac{1} {\Vert \mathrm{w} \Vert} \\ &= \max_{\mathrm{w}, b: (\mathrm{w} \cdot x_i + b) \geq 0} \frac{1}{\Vert \mathrm{w} \Vert} \quad \text{(min. reached)} \end{aligned}$$

As a result, the problem of finding margin is converted to finding the maximum value of the inverse of the norm of $\mathrm{w}$.

It is sort of optimization problem, but there are some constraints. Regardless of constraint, maximizing the inverse value is the same as the minimizing the value. So the overall optimization problem will be like this,

$$\max_{\mathrm{w}, b: (\mathrm{w} \cdot x_i + b) \geq 0} \frac{1}{\Vert \mathrm{w} \Vert} \\ \rightarrow \min_{\mathrm{w}, b} {1 \over 2} \Vert \mathrm{w} \Vert^2 \\ \text{subject to } y_i (\mathrm{w} \cdot x_i + b) \geq 1, i \in [1, m]$$

To get the value, we can apply the single constraint lagrange multiplier. Check the details in description of Lagrange multiplier

Linear non-separable problem

The problem is in linear non-separable case. Most of dataset found in real world often not linearly separable. In details, for any hyperplane, there exists $x_i$ such that $y_i[\mathrm{w} \cdot x_i + b] \not \geq 1$.

In that case, we need to relax the constraints to satisfy the problem. For doing this, we bring the concept of slack variable $\xi$. ($\xi \geq 0$)

$$y_i[ \mathrm{w} \cdot x_i + b] \geq 1 - \xi_i$$

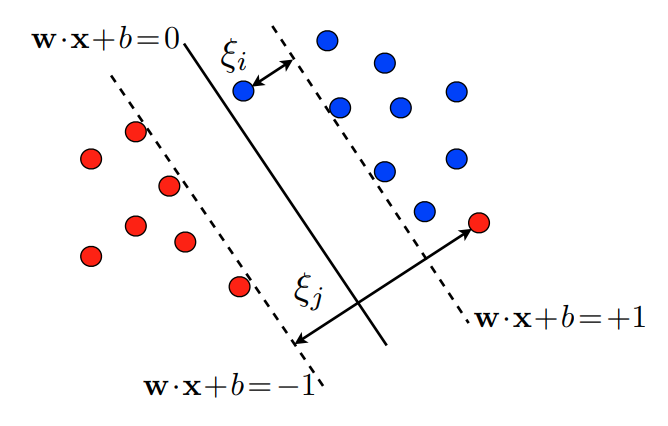
Soft margin hyperplane is the hyperplane created using a slack variable $\xi$. In the figure, the data points within the margin are the support vector. The blue dot has a smaller distance to the hyperplane than the margin, and the red dot is a misclassified outlier, both of them are used as support vectors (thanks to the relaxing constraint)

Note that the hyperplane expressed before used the contrained (or hard) margin. So that’s why it is called Hard margin hyperplane.

Actually, the difference between soft margin hyperplane and hard margin hyperplane is optimization problem. As you can saw in the soft margin hyperplane, we applied slack variable to relax the constraint. This slack variable is kind of error term. So in optimization problem, it will not only minimize the norm of $\mathrm{w}$, but also minimize the slack variable term:

$$\min_{\mathrm{w}, b, \xi} {1 \over 2} \Vert \mathrm{w} \Vert^2 + C \sum_{i = 1}^m \xi_i \\ \text{subject to }y_i(\mathrm{w} \cdot x_i + b) \geq 1 - \xi_i \wedge \xi_i \geq 0, i \in [1, m]$$

After all, the number of support vectors and the shape of hyperplane is dependent on the value of $C$. If $C$ is large, soft-margin does not allow the outliers, so it looks like hard-margin. Then, support vectors are rejected from finding hyperplane, and it will have a risk of overfitting. And if $C$ is small, lots of support vectors are accepted, and it occurs the underfitting problem.

Summary

An important concept in the linear classification model is the margin defined by the distance between the hyperplane and the nearest data point. At this post, it shows the process of finding hyperplane with maximizing the margin. Also, to handle the linearly non-separable classification problem, we brings the new term, slack variable($\xi$), and it can apply to find the soft margin.