Linear models in Deep Neural Networks
In this post, it will learn how linear models are used in deep neural networks. This post is the summary of "Mathematical principles in Machine Learning" offered from UNIST
Linear models in Deep Neural Networks
Linear models in Deep Neural Networks
Neural network has made remarkable progress in decades. But sometimes, neural network doesn’t work well as expected. For example, adding some unnoticable noise (e.g. gaussian noise) to image cannot be recognized by well-trained neural network, even if it looks the same to human.
Actually, the reason why the neural network doesn’t work isn’t explained well. If a network fails, it is difficult to understand what went wrong, and that’s why it is difficult to debug the network tuning.
One way to understand the behavior of neural network is visualization. It is simple look at how it classifies every possible data point, and help us to get a deeper intuition about the behavior of the neural network.
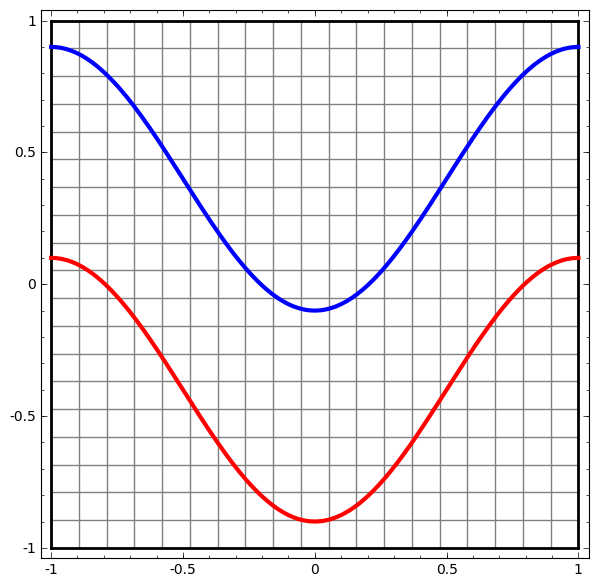
For example, consider about this case.
 [^1]
[^1]
Our goal is to classify two lines. And there is a simple neural network which has 2-inputs and 1 output. Can this neural network work? What about neural network with hidden layer?
When the data pass through the neural network, each layer transforms the data, creating a new representation. When the data reaches the last layer, the network will be draw the line to classify the data, and that is the hyperplane.
When the structure of neural network is complicated, it can express the summation of the non-linear activation with linear transformation. And the rule of linear transformation is to make data points in the last layer linearly separable.
So if the hidden layer is existed, the layer learns the new representation and it can make data to linearly separable.
Hidden layer can be described as a layer with non-linear activation function.
For example, consider about the hidden layer with $\tanh$ activation. ($\tanh (Wx + b)$) It consists of:
- A Linear transformation by the weight matrix $W$
- A Translation by the bias vector $b$
- $\tanh$ function for point-wise application
The visualization form of transform is like this:
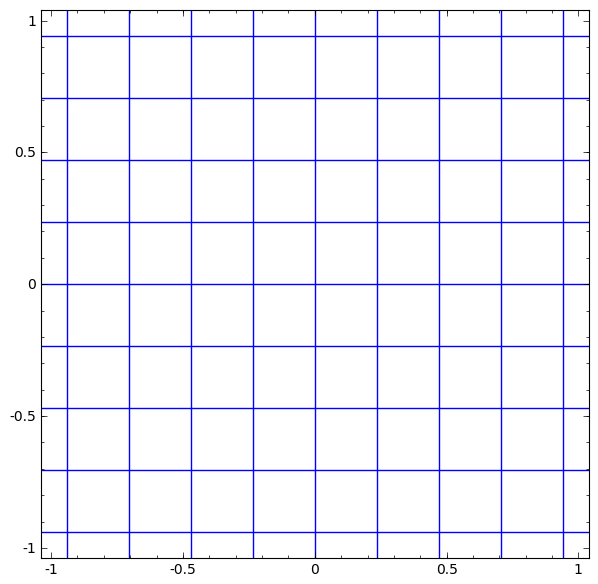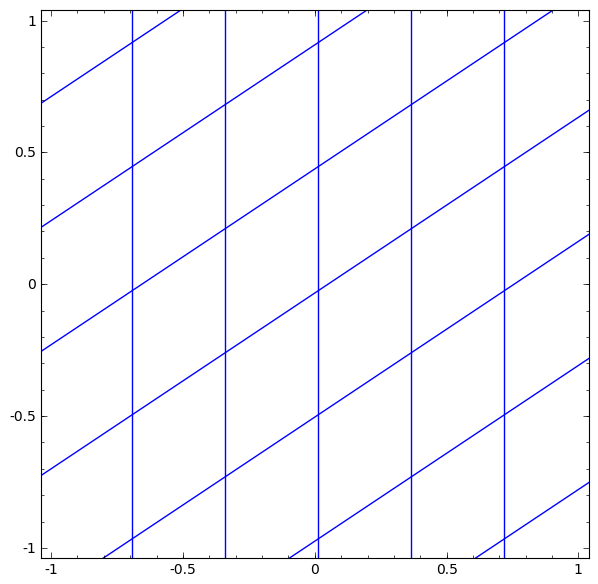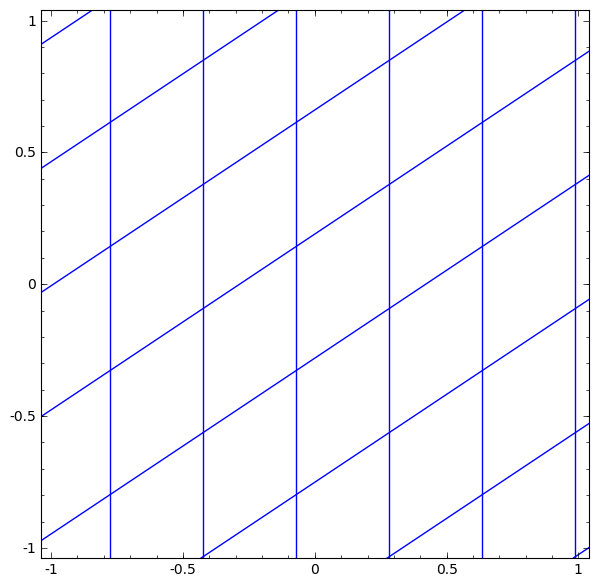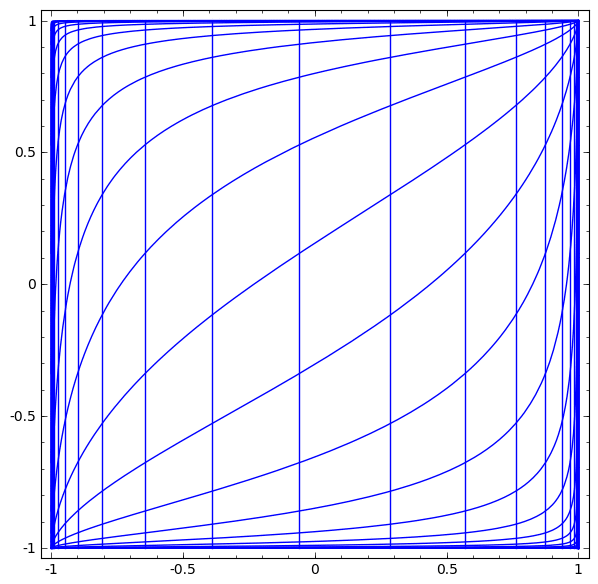 [^2]
[^2]
Another example can be found from here,
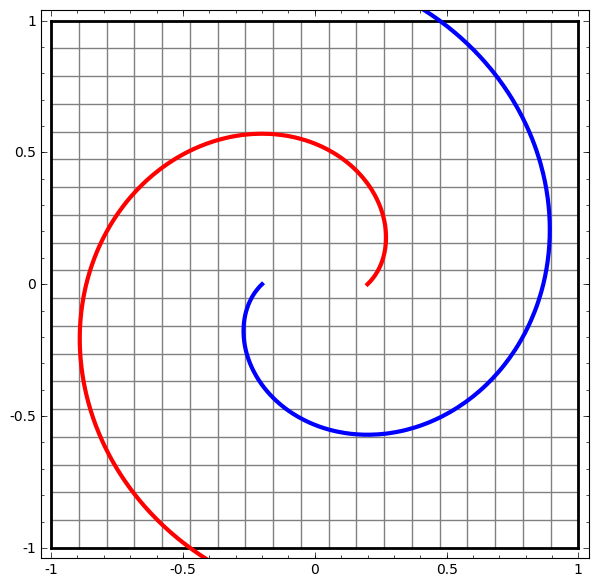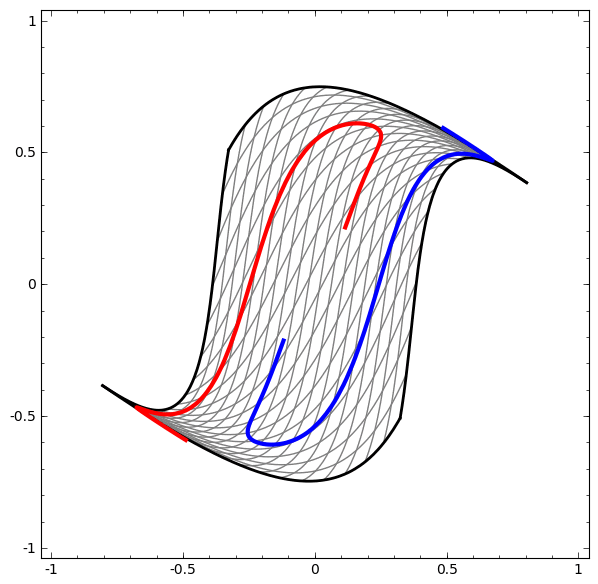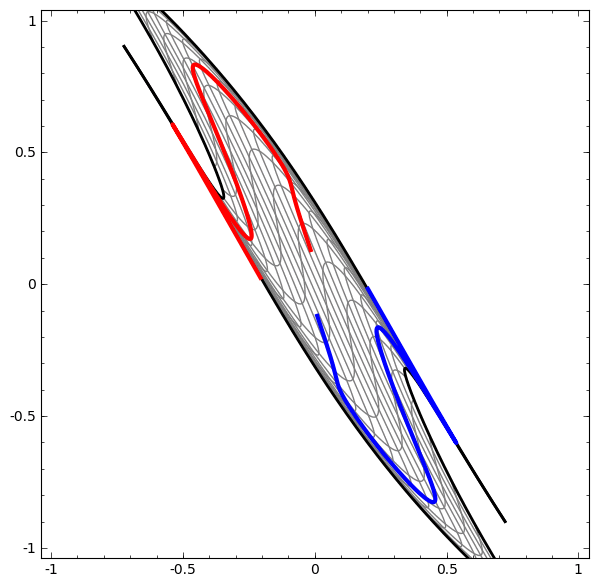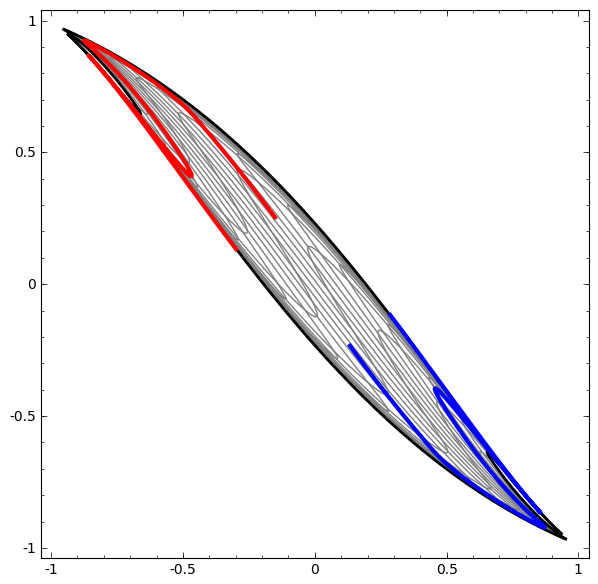 [^3]
[^3]
Affine transformation is the point-wise application of a monotone non-linear activation function. With hidden layer, it learns the new representation of data point to be linearly separable.
Summary
In this post, it explains the rule of linear model in deep neural network. The simple neural network (or perceptron) cannot handle the raw represention of data. But with hidden layer (and activation function), it can transform the dataset to be linear separable, so it works for classification.
[^1] [^2] [^3]: Figure from christopher olah’s post