Matrix Decomposition

Matrix Decomposition

Problem of Matrix Decomposition

Matrix decomposition is the method for approximating the observation matrix $Y$ by the product of dictionary matrix $D$ and $X$. Depending on the constraint for $D$ and $X$, it introduced four specific methods:

Sparse Coding (SC)
Principal Component Analysis (PCA)
Independent Component Analysis (ICA)
Non-negative Matrix Factorization (NMF)

Sparse Coding

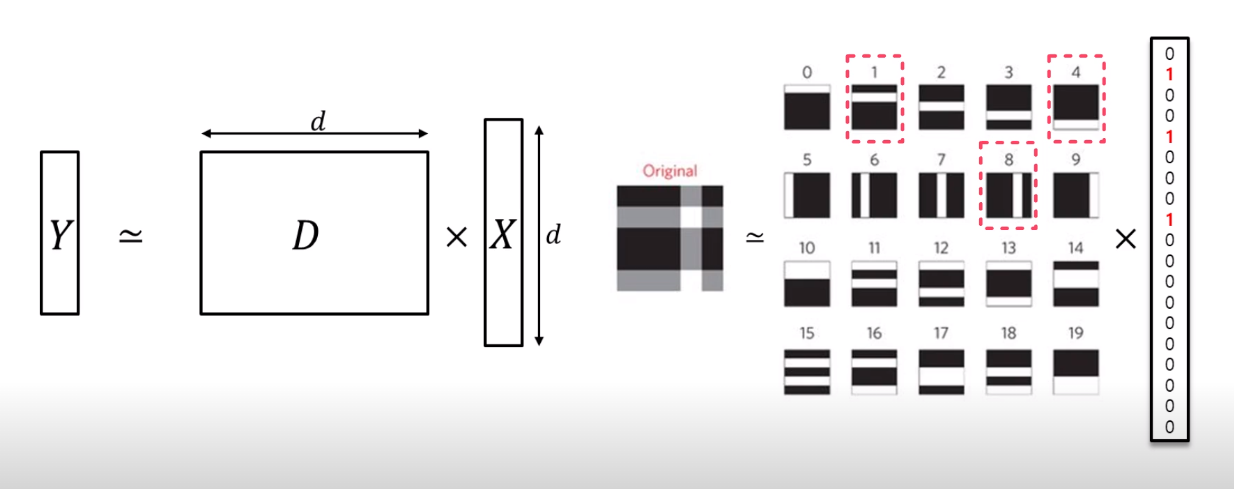
The purpose of Sparse Coding is the same as Matrix decomposition. It also tries to approximate observation matrix $Y$ by product of $D$ and $X$. Specifically, like this:

Y_{(m \times n)} \cong D_{(m \times d)} X_{(d \times n)}

Mentioned earlier, each matrix decomposition has some constraints. In Sparse Coding, it has two constraints that dictionary matrix $D$ must be row full-rank matrix. That is, the dimension of data in $D$ ($m$) is smaller than the dimension of basis ($d$). It is also called “fat-matrix”.(or overcomplete)

Another constraint is that the matrix $X$ must be a sparse matrix, so each row and column in $X$ should be sparse. With these constraints, our data $Y$ can be represented by the sparse combination of basis.

Suppose that $D$ is fat-matrix. ($m \leq d$) Then there exist infinitely many ways to represent $Y \cong D X$. So to solve this problem, $X$ must be sparse. So how can we make $X$ to be sparse?

Let’s bring the criteria of Sparse representation.

\min_{D, X} \Big[ \Vert Y - DX \Vert_2 + \lambda \Vert X \Vert_p \Big] \quad \text{where } p \in \{0, 1\}

At first, we assume the constraint that the norm of $X$ to be small while the multiplication of $D$ and $X$ to be similar to $Y$.(and that’s the way to minimize the criteria)

Usually, $L_0$ or $L_1$ norm is used to make $X$ sparse. In the previous post, $L_0$ norm is the number of non-zero elements in the matrix, and $L_1$ norm is the sum of absolute values of elements in the matrix. When we minimize the $L_0$ norm, the number of non-zero element will also reduce, and it makes $X$ to be sparse. If we consider to minimize the $L_1$ norm, it makes the geometric nature of absolute values to be zero, so it also makes the $X$ sparse.

But what if the $X$ is very very small? It means that dictionary matrix $D$ to be very large, and it may incur the lack of useful information. To prevent this, we need to add constraint for $D$,

\text{subject to } \Vert D \Vert^2 \leq C \quad \text{for some } C

Through this, it prevents the elements in $D$ become large and we can get resonable $X$.

sparse coding ¹

In the example, $Y$ can be represented with the product of $D$ and $X$. And instead of using whole data from $D$, we can select meaningful data with $X$. As a result, we can represent the observation matrix $Y$ with the sparse combination of simple basis through Sparse Coding.

Principal Component Analysis

Principal Component Analysis (PCA for short) is one of well-known dimensionality reduction method. While the dimension is reduced, it occurs the matrix decomposition, So PCA is also considered as a matrix decomposition method.

The main purpose of PCA is to find unit vector $u$ such that maximizes the variance of projections. Usually, high variance tends the data to be more separable. So it requires to find new basis for representing data.

Suppose that we have an observation data $Y$ with zero mean and unit variance. In this case, the variance of projected data is calculated like this:

\begin{aligned} \frac{1}{n} \sum_{i=1}^n (u^T y_i)^2 &= \frac{1}{n} \sum_{i=1}^n (y_i^T u)^2 \\ &= \frac{1}{n} \sum_{i=1}^n (y_i^Tu)^T(y_i^T u) \\ &= \frac{1}{n} \sum_{i=1}^n u^T y_i y_i^T u \\ &= u^T \Big( \frac{1}{n}\sum_{i=1}^n y_i y_i^T\Big)u \\ &= u^T \Sigma u \end{aligned} \\ \Sigma = \frac{1}{m}XX^T \quad \text{: sample covariance matrix}

So to apply PCA, we maximize the variance,

\max_u u^T \Sigma u

Here, we can add the constraint.

\text{subject to } u^T u = 1

In this case, $u$ is the eigenvector of the largest eigenvalue of covariance matrix $\Sigma$

Note: The form $\Sigma = U \Lambda U^T$ is called eigen analysis

Through this, we can know that finding the new basis is related on the eigen analysis of sample covariance matrix. And Eigen vector matrix $U$ of the covariance matrix $\Sigma$ is unit vector matrix. Also, Eigen value matrix $\Lambda$ of the covariance matrix is related to the relative magnitude of variance, and it is the significance of each unit vector.

Anyway, the representation of PCA with the sparse modeling can be expressed,

\min_{D, X} \underbrace{\Vert Y - DX \Vert_2}_{L(Y, D, X)} + \underbrace{\Vert D^TD-I \Vert + \Vert X^TX - \Sigma \Vert_2}_{\Psi(D, X)}

Here, $D$ is diagonal matrix. It also has constraints

$D$ is column full-rank
Column vectors $d_i, d_j$ of $D$ are orthonormal
Row vectors $x_i, x_j$ of $X$ are orthogonal

Focusing on the eigen analysis, if $YY^T = U \Lambda U^T$, $D$ can be unit vector($U$), and $X$ is $U^TY$. That means our data can be represented by linear combination of eigen vector and projected coefficient.

Independent Component Analysis (ICA)

Independent Component Analysis (ICA for short) is the computational method for separating obervations into linear combination of subcomponents.This subcomponents are also called the source, and it assume that each source is independent.

At first, Let’s define the notation. $Y$ is the observation matrix that each row vector $y_i$ of $Y$ corresponds to an observation from independent sources. And $D$ (we called it Dictionary matrix previously) is mixing matrix, each element of matrix represent the mixing ration between each sources. $X$ is Source matrix, its row vector $x_i, x_j$ are independent.

In ICA, the goal is same as previous one. We want to approximate $Y$ with product of $D$ and $X$. The first procedure of ICA is whitening the observation, meaning that makes the data uncorrelated each other, and have unit vector. In this step, mean shift is occurred,

Y \leftarrow Y - \mathbb{E}[Y]

Using this, we make the covariance matrix

\Sigma = cov(Y) = \mathbb{E}[YY^T] \\ = D \mathbb{E}[XX^T] D^T = D D^T

Then we perform the eigen analysis, and generate the whitening matrix $Q = \Lambda^{-1/2} U^T$. Using this whitening matrix, we can also make $D’$ and $Y’$ applying $Q$,

\begin{aligned} D'& = QD \\ Y' &= QY = QDX = D'X \end{aligned}

Calculating covariance of $Y’$ we can see that it is Identity matrix $I$,

\begin{aligned} cov(Y') &= \mathbb{E}[Y'{Y'}^T] \\ &= Q D \mathbb{E}[X X^T] D^T Q^T \\ &= Q D D^T Q^T = I\end{aligned}

The second procedure is to optimize the transformation of the whitened matrix $Y’$. Its expression may be difficult but it is just simply rotate the joint density of $Y’$. If we optimize it, it tends to maximize the non-normality of the marginal density.

Non-negative Matrix Factorization

Non-negative Matrix Factorization (NMF for short) has same goal with other matrix decomposition. But there is another constraint that the matrices $Y, D, X$ are all non-negative. It means tha all components are additive, and makes the input be represented by pure addition of basis in $D$ so that each basis of $D$ can represent local parts of the input $Y$.

One important attribute of NMF distinctive with other methods is that NMF enables to explain the data with its parts. In basis of dictionary matrix in PCA or ICA, it is difficult to explain intuitively. On the other hands, NMF represents the data with addition of localized features thanks to the non-negativity of each matrix as there is no subtraction available.

Summary

In this post, it introduced four common matrix decomposition method. Each method has each constraint. There are some mathematical intuition for each proof like eigen analysis. All method can be used for representing $Y$ with sparse modeling.

Figure from “Sparse coding with memristor networks” Sheridan et al. ↩