Causality
In this post, it will be explained about what the causality is, such as casual graphical model and temporal causality. This post is the summary of "Mathematical principles in Machine Learning" offered from UNIST.
Causality
Introduction to Causality
Causality, also referred to as causation, is what connect one process (cause) with another process (effect).

There are common confusion between association and causation. It is easy to understand the difference by example. Famous example is the relationship between Chocolate and Nobel prize winner. There was study result that the place where the chocolate consumption is high, won more nobel prize. In this case, chocolate consumption affects the the nobel prize winner? Actually, it is not. The truth is that two quantities (chocolate consumption and nobel prize winner) have steadily increased over time due to respective local conditions, which is not related any further. As a result, these two unrelated time trends induce an association. So in this case, we can tell that there is an association between the chocolate consumption in time and the nobel prize winner trend in time.
We can draw the relationship between the state $X$ and state $Y$.
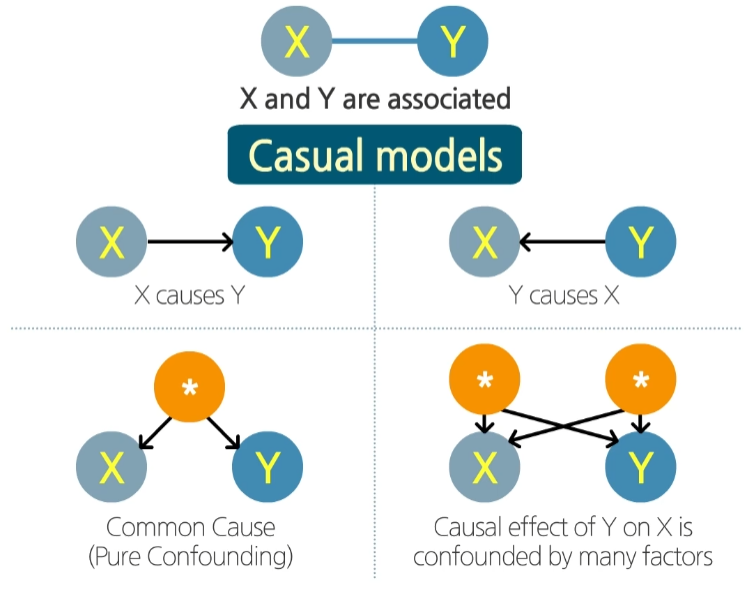
The mention of association between $X$ and $Y$ can be explained in 4 causal models.
- $X$ causes $Y$
- And $Y$ causes $X$
- There is common cause which occurs state $X$ and state $Y$. (Usually, it is called confounding)
- There are many confounding factors which occurs state $X$ and state $Y$.
Practically speaking, the word “$T$ causes $Y$” means that changing $T$ leads to a change in $Y$ keeping everything else constant, and vice versa. In this case, causal effect is the magnitude by which $Y$ is changed by a unit change in $T$.
Three layers of Causal Hierarchy
More concisely, we can define the level of causation in 3 layers.
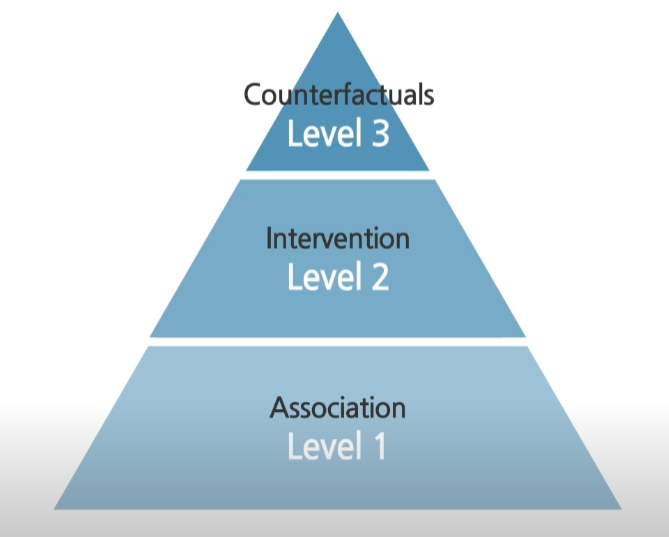
First level is Association. Here, we just only consider statistical relationship. We can directly infered from the observed data from conditional expectations. As you notice from the word, causal information is not required, questions in this hierarchy are placed at the lowest level of the hierarchy. So when we mention about association, it comes with conditional probability ($P(Y \vert X)$). In short, association cares observation such as “what is” and “How would seeing $X$ change our belief in $Y$?”
- Specification: $p(X), p(Y \vert X)$
- Joint Distribution: $p(X, Y)$
- Inferences: $p(X), p(Y), p(Y \vert X) p(X \vert Y)$
Second level is Intervention. Unlike association, intervention includes not only seeing what is, but changing what we see as sort of interventional inference. Usually, it includes action (expressed with $do(x)$). So when we see the comment of “perfect intervention”, it means that it is controlled experiment that an event is specifically set in some conditions. Mathmatically, it can express like this,
It is the probability of event $Y = y$ given that we intervene and set the value of $X$ to $x$ and subsequently observe event $Z = z$.
- Specification: $p(X), p(Y \vert X)$
- Joint distribution: $p(X, Y)$
- Inferences: $p(Y \vert do(X = x))$
The final level is Counterfactuals. And it includes interventional and associational questions. If we have a model that can answer counterfactual queries, we can also answer questions about interventions and observations. The mathematical symbol is like this,
It is the probability that event $Y = y$ would be observed hand $X$ been $x$, given that we actually observed $X$ to be $x’$ nad $Y$ to be $y’$.
- Specification: $p(X), p(Y \vert X)$
- Joint distribution: $p(X, Y)$
- Inferences: $p(Y_x = y \vert X = x’, Y = y’) = p(Y = y \vert X = x’, Y = y’, do(X = x))$
Summary
In this post, we covered what causality is and why it is important. And we briefly looked the three layers of causal hierarchy, Association, Intervention, and Counterfactuals.