Minimizing Kullback-Leibler Divergence
In this post, we will see how the KL divergence can be computed between two distribution objects, in cases where an analytical expression for the KL divergence is known. This is the summary of lecture "Probabilistic Deep Learning with Tensorflow 2" from Imperial College London.
import tensorflow as tf
import tensorflow_probability as tfp
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from IPython.display import HTML, Image
tfd = tfp.distributions
tfpl = tfp.layers
tfb = tfp.bijectors
plt.rcParams['figure.figsize'] = (10, 6)
plt.rcParams["animation.html"] = "jshtml"
plt.rcParams['animation.embed_limit'] = 2**128
print("Tensorflow Version: ", tf.__version__)
print("Tensorflow Probability Version: ", tfp.__version__)
scale_tril = tfb.FillScaleTriL()([-0.5, 1.25, 1.])
scale_tril
p = tfd.MultivariateNormalTriL(loc=0., scale_tril=scale_tril)
p
q = tfd.MultivariateNormalDiag(loc=[0., 0.])
q
tfd.kl_divergence(q, p)
q = tfd.MultivariateNormalDiag(
loc=tf.Variable(tf.random.normal([2])),
scale_diag=tfp.util.TransformedVariable(tf.random.uniform([2]), bijector=tfb.Exp())
)
q
tfd.kl_divergence(q, p)
@tf.function
def loss_and_grads(q_dist):
with tf.GradientTape() as tape:
loss = tfd.kl_divergence(q_dist, p)
return loss, tape.gradient(loss, q_dist.trainable_variables)
optimizer = tf.keras.optimizers.Adam()
for i in range(20):
loss, grads = loss_and_grads(q)
optimizer.apply_gradients(zip(grads, q.trainable_variables))
print(loss)
tf.random.set_seed(41)
p_mu = [0., 0.]
p_L = tfb.Chain([tfb.TransformDiagonal(tfb.Softplus()),
tfb.FillTriangular()])(tf.random.uniform([3]))
p = tfd.MultivariateNormalTriL(loc=p_mu, scale_tril=p_L)
p
def plot_density_contours(density, X1, X2, contour_kwargs, ax=None):
'''
Plots the contours of a bivariate TensorFlow density function (i.e. .prob()).
X1 and X2 are numpy arrays of mesh coordinates.
'''
if ax==None:
_, ax = plt.subplots(figsize=(7, 7))
X = np.hstack([X1.flatten()[:, np.newaxis], X2.flatten()[:, np.newaxis]])
density_values = np.reshape(density(X).numpy(), newshape=X1.shape)
ax.contour(X1, X2, density_values, **contour_kwargs)
return(ax)
x1 = np.linspace(-5, 5, 1000)
x2 = np.linspace(-5, 5, 1000)
X1, X2 = np.meshgrid(x1, x2)
f, ax = plt.subplots(1, 1, figsize=(7, 7))
# Density contours are linearly spaced
contour_levels = np.linspace(1e-4, 10**(-0.8), 20) # specific to this seed
ax = plot_density_contours(p.prob, X1, X2,
{'levels':contour_levels,
'cmap':'cividis'}, ax=ax)
ax.set_xlim(-5, 5); ax.set_ylim(-5, 5);
ax.set_title('Density contours of target distribution, $p$')
ax.set_xlabel('$x_1$'); ax.set_ylabel('$x_2$')
plt.show()
tf.random.set_seed(41)
q = tfd.MultivariateNormalDiag(loc=tf.Variable(tf.random.normal([2])),
scale_diag=tfp.util.TransformedVariable(tf.random.uniform([2]),
bijector=tfb.Exp()))
q
@tf.function
def loss_and_grads(dist_a, dist_b):
with tf.GradientTape() as tape:
loss = tfd.kl_divergence(dist_a, dist_b)
return loss, tape.gradient(loss, dist_a.trainable_variables)
from matplotlib import animation
fig, ax1 = plt.subplots(figsize=(7, 7))
num_train_steps = 250
opt = tf.keras.optimizers.Adam(learning_rate=.01)
last_q_loss = 0
def animate(i):
ax1.clear()
global last_q_loss
# Compute the KL divergence and its gradients
q_loss, grads = loss_and_grads(q, p)
# Update the trainable variables using the gradients via the optimizer
opt.apply_gradients(zip(grads, q.trainable_variables))
X = np.hstack([X1.flatten()[:, np.newaxis], X2.flatten()[:, np.newaxis]])
density_values = np.reshape(p.prob(X).numpy(), newshape=X1.shape)
ax1.contour(X1, X2, density_values, levels=contour_levels, cmap='cividis', alpha=0.5)
density_values = np.reshape(q.prob(X).numpy(), newshape=X2.shape)
ax1.contour(X1, X2, density_values, levels=contour_levels, cmap='plasma')
ax1.set_title('Density contours of $p$ and $q$\n' +
'Iteration ' + str(i + 1) + '\n' +
'$D_{KL}[q \ || \ p] = ' +
str(np.round(q_loss.numpy(), 4)) + '$',
loc='left')
last_q_loss = q_loss.numpy()
ani = animation.FuncAnimation(fig, animate, frames=num_train_steps)
plt.close()
ani.save('./image/kl_qp.gif', writer='imagemagick', fps=30)
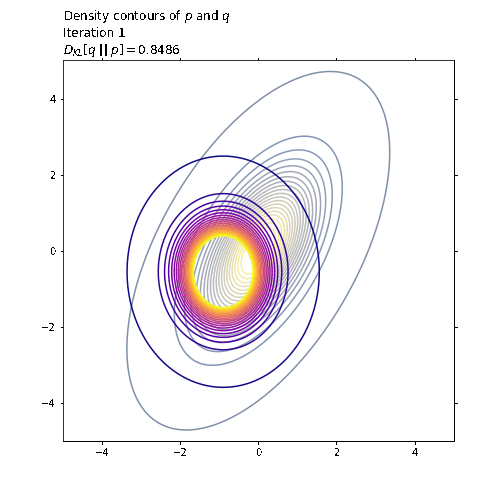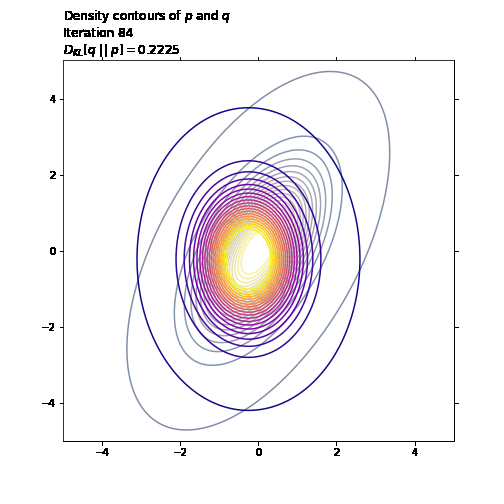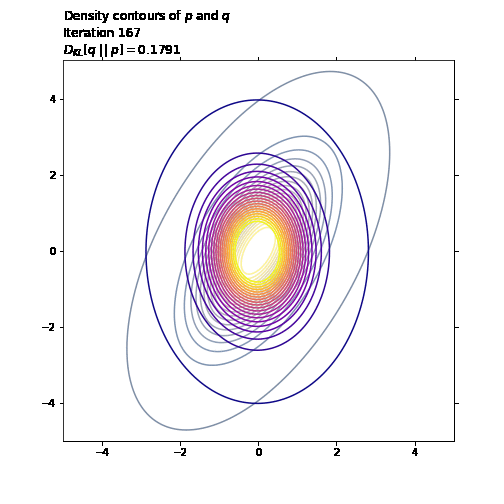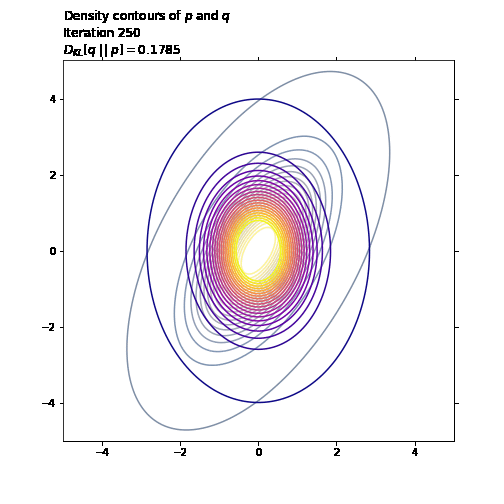
tf.random.set_seed(41)
q_rev = tfd.MultivariateNormalDiag(loc=tf.Variable(tf.random.normal([2])),
scale_diag=tfp.util.TransformedVariable(tf.random.uniform([2]), bijector=tfb.Exp()))
q_rev
@tf.function
def loss_and_grads(dist_a, dist_b, reverse=False):
with tf.GradientTape() as tape:
if not reverse:
loss = tfd.kl_divergence(dist_a, dist_b)
else:
loss = tfd.kl_divergence(dist_b, dist_a)
return loss, tape.gradient(loss, dist_a.trainable_variables)
fig, ax1 = plt.subplots(figsize=(7, 7))
num_train_steps = 250
opt = tf.keras.optimizers.Adam(learning_rate=.01)
last_q_rev_loss = 0
def animate(i):
ax1.clear()
global last_q_rev_loss
# Compute the KL divergence and its gradients
q_rev_loss, grads = loss_and_grads(q_rev, p, reverse=True)
# Update the trainable variables using the gradients via the optimizer
opt.apply_gradients(zip(grads, q_rev.trainable_variables))
X = np.hstack([X1.flatten()[:, np.newaxis], X2.flatten()[:, np.newaxis]])
density_values = np.reshape(p.prob(X).numpy(), newshape=X1.shape)
ax1.contour(X1, X2, density_values, levels=contour_levels, cmap='cividis', alpha=0.5)
density_values = np.reshape(q_rev.prob(X).numpy(), newshape=X2.shape)
ax1.contour(X1, X2, density_values, levels=contour_levels, cmap='plasma')
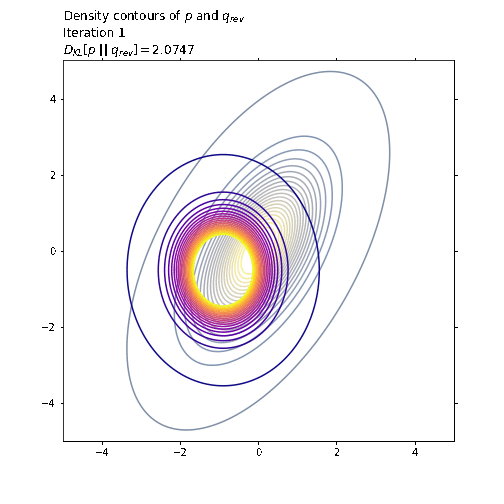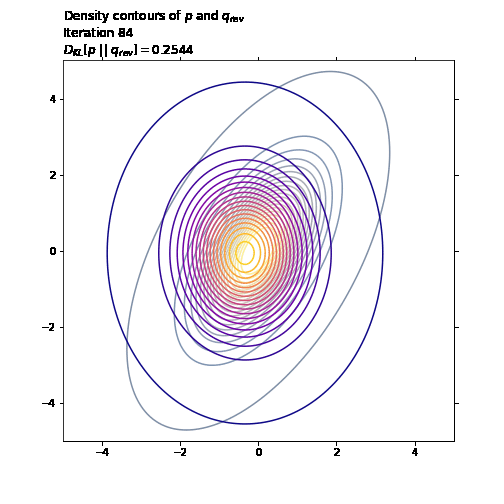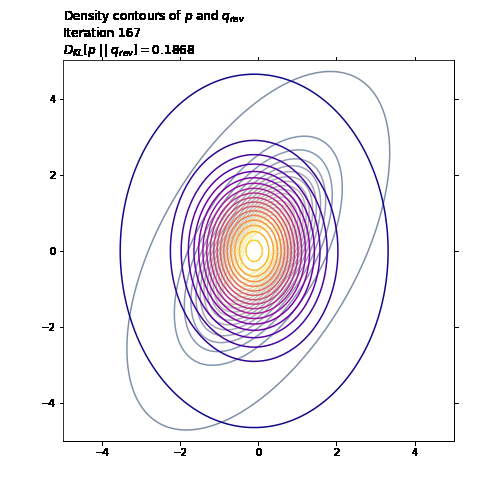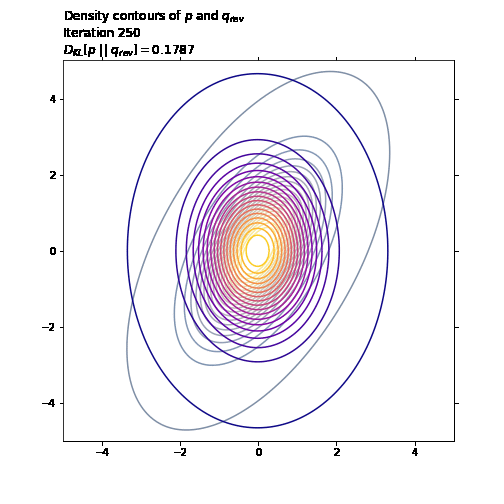
ax1.set_title('Density contours of $p$ and $q_{rev}$\n' +
'Iteration ' + str(i + 1) + '\n' +
'$D_{KL}[p \ || \ q_{rev}] = ' +
str(np.round(q_rev_loss.numpy(), 4)) + '$',
loc='left')
last_q_rev_loss = q_rev_loss.numpy()
ani = animation.FuncAnimation(fig, animate, frames=num_train_steps)
plt.close()
ani.save('./image/kl_pq.gif', writer='imagemagick', fps=30)
f, axs = plt.subplots(1, 2, figsize=(15, 7))
axs[0] = plot_density_contours(p.prob, X1, X2,
{'levels':contour_levels,
'cmap':'cividis', 'alpha':0.5}, ax=axs[0])
axs[0] = plot_density_contours(q.prob, X1, X2,
{'levels':contour_levels,
'cmap':'plasma'}, ax=axs[0])
axs[0].set_title('Density contours of $p$ and $q$\n' +
'$D_{KL}[q \ || \ p] = ' + str(np.round(last_q_loss, 4)) + '$',
loc='left')
axs[1] = plot_density_contours(p.prob, X1, X2,
{'levels':contour_levels,
'cmap':'cividis', 'alpha':0.5}, ax=axs[1])
axs[1] = plot_density_contours(q_rev.prob, X1, X2,
{'levels':contour_levels,
'cmap':'plasma'}, ax=axs[1])
axs[1].set_title('Density contours of $p$ and $q_{rev}$\n' +
'$D_{KL}[p \ || \ q_{rev}] = ' + str(np.round(last_q_rev_loss, 4)) + '$',
loc='left')
plt.show()