Basics of deep learning and neural networks
In this chapter, you'll become familiar with the fundamental concepts and terminology used in deep learning, and understand why deep learning techniques are so powerful today. You'll build simple neural networks and generate predictions with them. This is the Summary of lecture "Introduction to Deep Learning in Python", via datacamp.
- Basics of deep learning and neural networks
- Forward propagation
- Activation functions
- Deeper networks
import numpy as np
import pandas as pd
Coding the forward propagation algorithm
In this exercise, you'll write code to do forward propagation (prediction) for your first neural network:
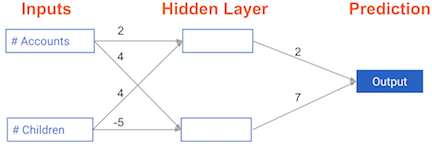
Each data point is a customer. The first input is how many accounts they have, and the second input is how many children they have. The model will predict how many transactions the user makes in the next year.
input_data = np.array([3, 5])
weights = {'node_0': np.array([2, 4]),
'node_1': np.array([ 4, -5]),
'output': np.array([2, 7])}
node_0_value = (input_data * weights['node_0']).sum()
# Calculate node 1 value: node_1_value
node_1_value = (input_data * weights['node_1']).sum()
# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_value, node_1_value])
# Calculate output: output
output = (hidden_layer_outputs * weights['output']).sum()
# Print output
print(output)
The Rectified Linear Activation Function
An "activation function" is a function applied at each node. It converts the node's input into some output.
The rectified linear activation function (called ReLU) has been shown to lead to very high-performance networks. This function takes a single number as an input, returning 0 if the input is negative, and the input if the input is positive.
def relu(input):
'''Define your relu activatino function here'''
# Calculate the value for the output of the relu function: output
output = max(0, input)
# Return the value just calculate
return output
# Calculate node 0 value: node_0_output
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)
# Calculate node 1 value: node_1_output
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)
# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])
# Calculate model output (do not apply relu)
model_output = (hidden_layer_outputs * weights['output']).sum()
# Print model output
print(model_output)
Applying the network to many observations/rows of data
You'll now define a function called predict_with_network() which will generate predictions for multiple data observations, which are pre-loaded as input_data. As before, weights are also pre-loaded. In addition, the relu() function you defined in the previous exercise has been pre-loaded.
input_data = [np.array([3, 5]), np.array([ 1, -1]),
np.array([0, 0]), np.array([8, 4])]
def predict_with_network(input_data_row, weights):
# Calculate node 0 value
node_0_input = (input_data_row * weights['node_0']).sum()
node_0_output = relu(node_0_input)
# Calculate node 1 value
node_1_input = (input_data_row * weights['node_1']).sum()
node_1_output = relu(node_1_input)
# Put node values into array: hidden_layer_outputs
hidden_layer_outputs = np.array([node_0_output, node_1_output])
# Calculate model output
input_to_final_layer = (hidden_layer_outputs * weights['output']).sum()
model_output = relu(input_to_final_layer)
# Return model output
return(model_output)
# Create empty list to store prediction results
results = []
for input_data_row in input_data:
# Append prediction to results
results.append(predict_with_network(input_data_row, weights))
# Print results
print(results)
Deeper networks
- Representation learning
- Deep networks internally build representations of patterns in the data
- Partially replace the need for feature engnerring
- Subsequent layers build increasingly sophisticated representatios of raw data
- Deep learning
- Modeler doesn't need to specify the interactions
- When you train the model, the neural network gets weights that find the relevant patterns to make better predictions
Multi-layer neural networks
In this exercise, you'll write code to do forward propagation for a neural network with 2 hidden layers. Each hidden layer has two nodes. The input data has been preloaded as input_data. The nodes in the first hidden layer are called node_0_0 and node_0_1. Their weights are pre-loaded as weights['node_0_0'] and weights['node_0_1'] respectively.
The nodes in the second hidden layer are called node_1_0 and node_1_1. Their weights are pre-loaded as weights['node_1_0'] and weights['node_1_1'] respectively.
We then create a model output from the hidden nodes using weights pre-loaded as weights['output'].
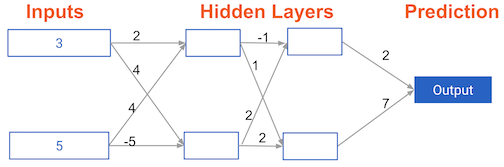
input_data = np.array([3, 5])
weights = {'node_0_0': np.array([2, 4]),
'node_0_1': np.array([ 4, -5]),
'node_1_0': np.array([-1, 2]),
'node_1_1': np.array([1, 2]),
'output': np.array([2, 7])}
def predict_with_network(input_data):
# Calculate node 0 in the first hidden layer
node_0_0_input = (input_data * weights['node_0_0']).sum()
node_0_0_output = relu(node_0_0_input)
# Calculate node 1 in the first hidden layer
node_0_1_input = (input_data * weights['node_0_1']).sum()
node_0_1_output = relu(node_0_1_input)
# Put node values into array: hidden_0_outputs
hidden_0_outputs = np.array([node_0_0_output, node_0_1_output])
# Calculate node 0 in the second hidden layer
node_1_0_input = (hidden_0_outputs * weights['node_1_0']).sum()
node_1_0_output = relu(node_1_0_input)
# Calculate node 1 in the second hidden layer
node_1_1_input = (hidden_0_outputs * weights['node_1_1']).sum()
node_1_1_output = relu(node_1_1_input)
# Put node values into array: hidden_1_outputs
hidden_1_outputs = np.array([node_1_0_output, node_1_1_output])
# Calculate model output: model_output
model_output = (hidden_1_outputs * weights['output']).sum()
# Return model_output
return model_output
output = predict_with_network(input_data)
print(output)