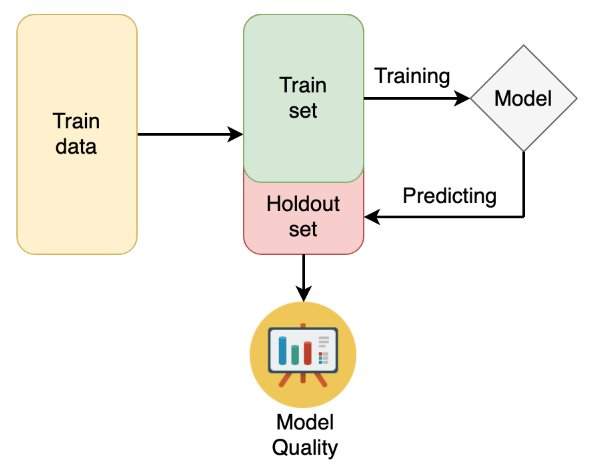
Dive into the Competition
Now that you know the basics of Kaggle competitions, you will learn how to study the specific problem at hand. You will practice EDA and get to establish correct local validation strategies. You will also learn about data leakage. This is the Summary of lecture "Winning a Kaggle Competition in Python", via datacamp.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize']=(10, 8)
Define a competition metric
Competition metric is used by Kaggle to evaluate your submissions. Moreover, you also need to measure the performance of different models on a local validation set.
For now, your goal is to manually develop a couple of competition metrics in case if they are not available in sklearn.metrics.
In particular, you will define:
- Mean Squared Error (MSE) for the regression problem:
$$ MSE = \frac{1}{N} \sum_{i=1}^{N}(y_i - \hat{y_i})^2 $$
- Logarithmic Loss (LogLoss) for the binary classification problem:
$$ LogLoss = -\frac{1}{N} \sum_{i = 1}^N (y_i \ln p_i + (1 - y_i) \ln (1 - p_i)) $$
sample = pd.read_csv('./dataset/sample_reg_true_pred.csv')
y_regression_true, y_regression_pred = sample['true'].to_numpy(), sample['pred'].to_numpy()
from sklearn.metrics import mean_squared_error
# Define your own MSE function
def own_mse(y_true, y_pred):
# Raise differences to the power of 2
squares = np.power(y_true - y_pred, 2)
# Find mean over all observations
err = np.mean(squares)
return err
print('Sklearn MSE: {:.5f}. '.format(mean_squared_error(y_regression_true, y_regression_pred)))
print('Your MSE: {:.5f}. '.format(own_mse(y_regression_true, y_regression_pred)))
sample_class = pd.read_csv('./dataset/sample_class_true_pred.csv')
y_classification_true, y_classification_pred = sample_class['true'].to_numpy(), sample_class['pred'].to_numpy()
from sklearn.metrics import log_loss
# Define your own LogLoss function
def own_logloss(y_true, prob_pred):
# Find loss for each observation
terms = y_true * np.log(prob_pred) + (1 - y_true) * np.log(1 - prob_pred)
# Find mean over all observations
err = np.mean(terms)
return -err
print('Sklearn LogLoss: {:.5f}'.format(log_loss(y_classification_true, y_classification_pred)))
print('Your LogLoss: {:.5f}'.format(own_logloss(y_classification_true, y_classification_pred)))
train = pd.read_csv('./dataset/taxi_train_chapter_4.csv')
test = pd.read_csv('./dataset/taxi_test_chapter_4.csv')
# Shapes of train and test data
print('Train shape:', train.shape)
print('Test shape:', test.shape)
# train head()
train.head()
train.fare_amount.describe()
train.passenger_count.value_counts()
EDA plots I
After generating a couple of basic statistics, it's time to come up with and validate some ideas about the data dependencies. Again, the train DataFrame from the taxi competition is already available in your workspace.
To begin with, let's make a scatterplot plotting the relationship between the fare amount and the distance of the ride. Intuitively, the longer the ride, the higher its price.
def haversine_distance(train):
data = [train]
lat1, long1, lat2, long2 = 'pickup_latitude', 'pickup_longitude', 'dropoff_latitude', 'dropoff_longitude'
for i in data:
R = 6371 #radius of earth in kilometers
#R = 3959 #radius of earth in miles
phi1 = np.radians(i[lat1])
phi2 = np.radians(i[lat2])
delta_phi = np.radians(i[lat2]-i[lat1])
delta_lambda = np.radians(i[long2]-i[long1])
#a = sin²((φB - φA)/2) + cos φA . cos φB . sin²((λB - λA)/2)
a = np.sin(delta_phi / 2.0) ** 2 + np.cos(phi1) * np.cos(phi2) * np.sin(delta_lambda / 2.0) ** 2
#c = 2 * atan2( √a, √(1−a) )
c = 2 * np.arctan2(np.sqrt(a), np.sqrt(1-a))
#d = R*c
d = (R * c) #in kilometers
return d
train['distance_km'] = haversine_distance(train)
# Draw a scatterplot
plt.scatter(x=train['fare_amount'], y=train['distance_km'], alpha=0.5);
plt.xlabel('Fare amount');
plt.ylabel('Distance, km');
plt.title('Fare amount based on the distance');
# Limit on the distance
plt.ylim(0, 50);
EDA plots II
Another idea that comes to mind is that the price of a ride could change during the day.
Your goal is to plot the median fare amount for each hour of the day as a simple line plot. The hour feature is calculated for you. Don't worry if you do not know how to work with the date features. We will explore them in the chapter on Feature Engineering.
train['pickup_datetime'] = pd.to_datetime(train.pickup_datetime)
train['hour'] = train.pickup_datetime.dt.hour
# Find median fare_amount for each hour
hour_price = train.groupby('hour', as_index=False)['fare_amount'].median()
# Plot the line plot
plt.plot(hour_price['hour'], hour_price['fare_amount'], marker='o');
plt.xlabel('Hour of the day');
plt.ylabel('Median fare amount');
plt.title('Fare amount based on day time');
plt.xticks(range(24));
We see that prices are a bit higher during the night. It is a good indicator that we should include the "hour" feature in the final model, or at least add a binary feature "is_night".
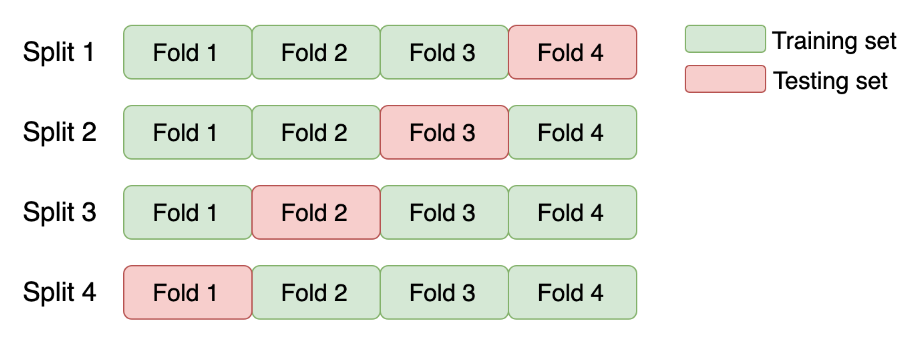
K-fold cross-validation
You will start by getting hands-on experience in the most commonly used K-fold cross-validation.
The data you'll be working with is from the "Two sigma connect: rental listing inquiries" Kaggle competition. The competition problem is a multi-class classification of the rental listings into 3 classes: low interest, medium interest and high interest. For faster performance, you will work with a subsample consisting of 1,000 observations.
You need to implement a K-fold validation strategy and look at the sizes of each fold obtained.
train = pd.read_csv('./dataset/twosigma_rental_train.csv')
from sklearn.model_selection import KFold
# Create a KFold object
kf = KFold(n_splits=3, shuffle=True, random_state=123)
# Loop through each split
fold = 0
for train_index, test_index in kf.split(train):
# Obtain training and test folds
cv_train, cv_test = train.iloc[train_index], train.iloc[test_index]
print("Fold: {}".format(fold))
print("CV train shape: {}".format(cv_train.shape))
print("Medium interest listings in CV train: {}\n".format(
sum(cv_train.interest_level == 'medium')
))
fold += 1
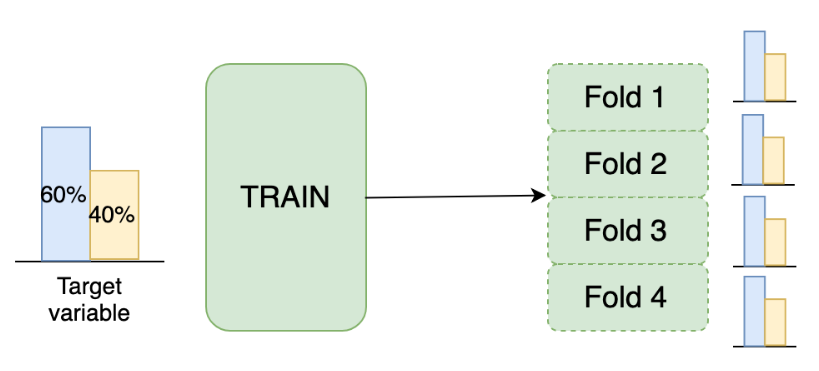
Stratified K-fold
As you've just noticed, you have a pretty different target variable distribution among the folds due to the random splits. It's not crucial for this particular competition, but could be an issue for the classification competitions with the highly imbalanced target variable.
To overcome this, let's implement the stratified K-fold strategy with the stratification on the target variable.
from sklearn.model_selection import StratifiedKFold
# Create a StratifiedKFold object
str_kf = StratifiedKFold(n_splits=3, shuffle=True, random_state=123)
# Loop through each split
fold = 0
for train_index, test_index in str_kf.split(train, train['interest_level']):
# Obtain training and test folds
cv_train, cv_test = train.iloc[train_index], train.iloc[test_index]
print('Fold: {}'.format(fold))
print('CV train shape: {}'.format(cv_train.shape))
print('Medium interest listings in CV train: {}\n'.format(
sum(cv_train.interest_level == 'medium')
))
fold += 1
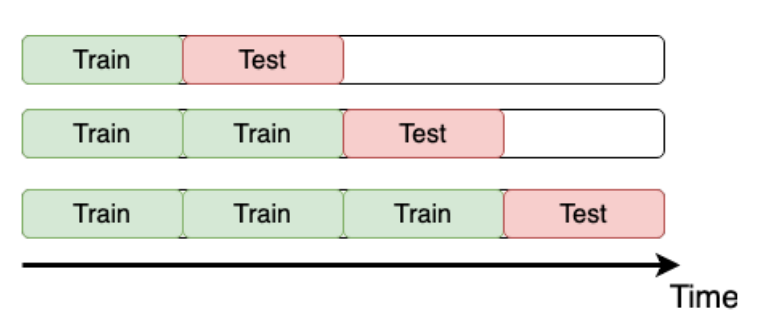
Time K-fold
Remember the "Store Item Demand Forecasting Challenge" where you are given store-item sales data, and have to predict future sales?
It's a competition with time series data. So, time K-fold cross-validation should be applied. Your goal is to create this cross-validation strategy and make sure that it works as expected.
train = pd.read_csv('./dataset/demand_forecasting_train_1_month.csv')
from sklearn.model_selection import TimeSeriesSplit
# Create TimeSeriesSplit object
time_kfold = TimeSeriesSplit(n_splits=3)
# sort train data by date
train = train.sort_values('date')
# Iterate through each split
fold = 0
for train_index, test_index in time_kfold.split(train):
cv_train, cv_test = train.iloc[train_index], train.iloc[test_index]
print('Fold :', fold)
print('Train date range: from {} to {}'.format(cv_train.date.min(), cv_train.date.max()))
print('Test date range: from {} to {}\n'.format(cv_test.date.min(), cv_test.date.max()))
fold += 1
Overall validation score
Now it's time to get the actual model performance using cross-validation! How does our store item demand prediction model perform?
Your task is to take the Mean Squared Error (MSE) for each fold separately, and then combine these results into a single number.
For simplicity, you're given get_fold_mse() function that for each cross-validation split fits a Random Forest model and returns a list of MSE scores by fold.
from sklearn.ensemble import RandomForestRegressor
def get_fold_mse(train, kf):
mse_scores = []
for train_index, test_index in kf.split(train):
fold_train, fold_test = train.loc[train_index], train.loc[test_index]
# Fit the data and make predictions
# Create a Random Forest object
rf = RandomForestRegressor(n_estimators=10, random_state=123)
# Train a model
rf.fit(X=fold_train[['store', 'item']], y=fold_train['sales'])
# Get predictions for the test set
pred = rf.predict(fold_test[['store', 'item']])
fold_score = round(mean_squared_error(fold_test['sales'], pred), 5)
mse_scores.append(fold_score)
return mse_scores
kf = TimeSeriesSplit(n_splits=3)
# Get MSE scores for each cross-validation split
mse_scores = get_fold_mse(train, kf)
print('Mean validation MSE: {:.5f}'.format(np.mean(mse_scores)))
print('MSE by fold: {}'.format(mse_scores))
print('Overall Validation MSE: {:.5f}'.format(np.mean(mse_scores) + np.std(mse_scores)))