Understanding and Improving Deep Convolutional Networks in Keras
There are many ways to improve training by neural networks. In this chapter, we will focus on our ability to track how well a network is doing, and explore approaches towards improving convolutional neural networks. This is the Summary of lecture "Image Processing with Keras in Python", via datacamp.
import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
(train_data, train_labels), (test_data, test_labels) = tf.keras.datasets.fashion_mnist.load_data()
train_data = train_data[(train_labels >= 0) & (train_labels < 3)][0:50].reshape(-1, 28, 28, 1)
train_labels = train_labels[(train_labels >= 0) & (train_labels < 3)][0:50]
train_labels = pd.get_dummies(train_labels).to_numpy()
test_data = test_data[(test_labels >= 0) & (test_labels < 3)][0:10].reshape(-1, 28, 28, 1)
test_labels = test_labels[(test_labels >= 0) & (test_labels < 3)][0:10]
test_labels = pd.get_dummies(test_labels).to_numpy()
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Conv2D, Flatten, MaxPool2D
img_rows, img_cols = 28, 28
model = Sequential()
model.add(Conv2D(4, kernel_size=2, activation='relu', input_shape=(img_rows, img_cols, 1)))
model.add(MaxPool2D(2))
model.add(Conv2D(8, kernel_size=3, activation='relu'))
model.add(Flatten())
model.add(Dense(3, activation='softmax'))
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
model.summary()
from tensorflow.keras.callbacks import ModelCheckpoint
checkpoint = ModelCheckpoint('weights.hdf5', monitor='val_loss', save_best_only=True)
# Train the model and store the training object (including modelCheckpoint callback)
training = model.fit(train_data, train_labels, epochs=3, batch_size=10, validation_split=0.2,
callbacks=[checkpoint])
# Extract the history from the training object
history = training.history
# Plot the training loss
plt.plot(history['loss'], label='train loss');
# Plot the validation loss
plt.plot(history['val_loss'], label='validation loss');
plt.legend();
Using stored weights to predict in a test set
Model weights stored in an hdf5 file can be reused to populate an untrained model. Once the weights are loaded into this model, it behaves just like a model that has been trained to reach these weights. For example, you can use this model to make predictions from an unseen data set (e.g. test_data).
model.load_weights('weights.hdf5')
# Predict from the first three images in the test data
# model.predict_classes(test_data) <- .predict_classes API will be decrepted
print(np.argmax(model.predict(test_data), axis=-1))
print(test_labels)
Regularization
- Dropout
- In each learning step:
- Select a subset of the units
- Ignore it in the forward pass
- And in the back-propagation of error
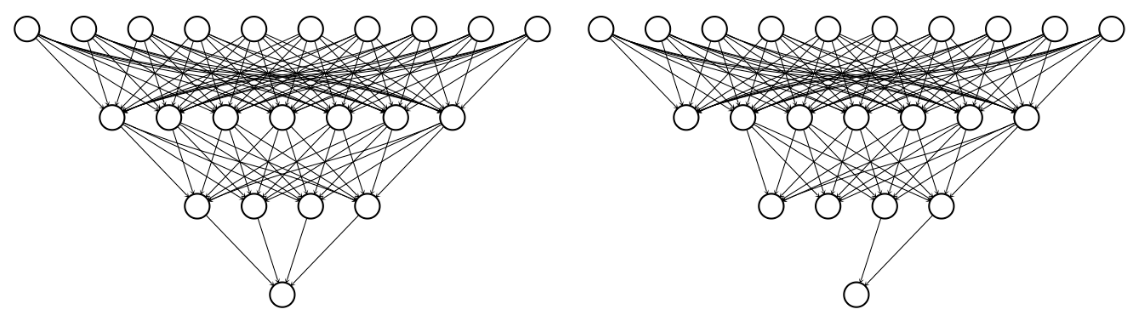
- In each learning step:
- Batch Normalization
- Rescale the outputs
- Disharmony between dropout and batch normalization
- Dropout tends to slow down learning, making it more incremental
- Batch Normalization tends to make learning go faster
- Their effects together may in fact each other.
Adding dropout to your network
Dropout is a form of regularization that removes a different random subset of the units in a layer in each round of training. In this exercise, we will add dropout to the convolutional neural network that we have used in previous exercises:
- Convolution (15 units, kernel size 2, 'relu' activation)
- Dropout (20%)
- Convolution (5 units, kernel size 2, 'relu' activation)
- Flatten
- Dense (3 units, 'softmax' activation)
from tensorflow.keras.layers import Dropout
model = Sequential()
# Add a convolutional layer
model.add(Conv2D(15, kernel_size=2, activation='relu', input_shape=(img_rows, img_cols, 1)))
# Add a dropout layer
model.add(Dropout(0.2))
# Add another convolutional layer
model.add(Conv2D(5, kernel_size=2, activation='relu'))
# Flatten and feed to output layer
model.add(Flatten())
model.add(Dense(3, activation='softmax'))
model.summary()
Add batch normalization to your network
Batch normalization is another form of regularization that rescales the outputs of a layer to make sure that they have mean 0 and standard deviation 1. In this exercise, we will add batch normalization to the convolutional neural network that we have used in previous exercises:
- Convolution (15 units, kernel size 2, 'relu' activation)
- Batch normalization
- Convolution (5 unites, kernel size 2, 'relu' activation)
- Flatten
- Dense (3 units, 'softmax' activation)
from tensorflow.keras.layers import BatchNormalization
model = Sequential()
# Add a convolutional layer
model.add(Conv2D(15, kernel_size=2, activation='relu', input_shape=(img_rows, img_cols, 1)))
# Add batch normalization layer
model.add(BatchNormalization())
# Add another convolutional layer
model.add(Conv2D(5, kernel_size=2, activation='relu'))
# Flatten and feed to output layer
model.add(Flatten())
model.add(Dense(3, activation='softmax'))
model.summary()
model = Sequential()
model.add(Conv2D(5, kernel_size=2, activation='relu', input_shape=(img_rows, img_cols, 1)))
model.add(Conv2D(15, kernel_size=2, activation='relu'))
model.add(MaxPool2D(2))
model.add(Flatten())
model.add(Dense(3, activation='softmax'))
model.summary()
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
checkpoint = ModelCheckpoint('weights_fasion.hdf5', monitor='val_loss', save_best_only=True)
model.fit(train_data, train_labels, epochs=3, validation_split=0.2, batch_size=10,
callbacks=[checkpoint]);
model.load_weights('weights_fasion.hdf5')
# Get the first convolutional layer from the model
c1 = model.layers[0]
# Get the weights of the first convolutional layer
weights1 = c1.get_weights()
# Pull out the first channel of the first kernel in the first layer
kernel = weights1[0][..., 0, 0]
print(kernel)
print(kernel.shape)
Visualizing kernel responses
One of the ways to interpret the weights of a neural network is to see how the kernels stored in these weights "see" the world. That is, what properties of an image are emphasized by this kernel. In this exercise, we will do that by convolving an image with the kernel and visualizing the result. Given images in the test_data variable, a function called extract_kernel() that extracts a kernel from the provided network, and the function called convolution() that we defined in the first chapter, extract the kernel, load the data from a file and visualize it with matplotlib.
def convolution(image, kernel):
kernel = kernel - kernel.mean()
result = np.zeros(image.shape)
for ii in range(image.shape[0]-2):
for jj in range(image.shape[1]-2):
result[ii, jj] = np.sum(image[ii:ii+2, jj:jj+2] * kernel)
return result
out = convolution(test_data[3, :, :, 0], kernel)
def plot_comparison(img_original, img_filtered, img_title_filtered):
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(10, 8), sharex=True, sharey=True)
ax1.imshow(img_original)
ax1.set_title('Original')
ax1.axis('off')
ax2.imshow(img_filtered)
ax2.set_title(img_title_filtered)
ax2.axis('off')
plot_comparison(test_data[3, :, :, 0], out, 'applying kernel')