Basic Time Series Metrics & Resampling
A Summary of lecture "Manipulating Time Series Data in Python", via datacamp
- Compare time series growth rates
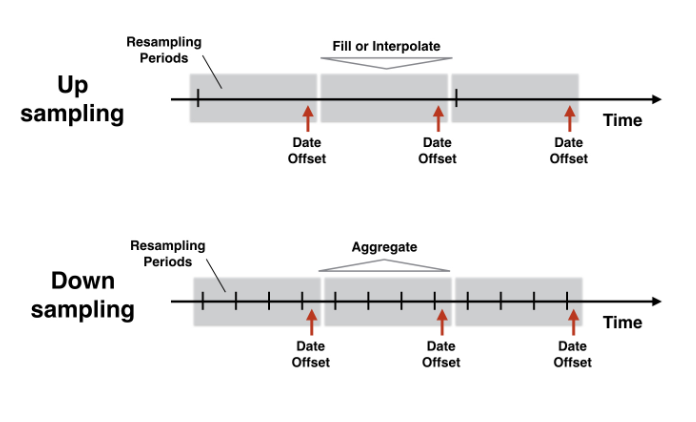
- Changing the time series frequency: resampling
- Upsampling & interpolation with .resample()
- Downsampling & aggregation
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['figure.figsize'] = (10, 5)
Compare time series growth rates
- Comparing stock performance
- Stock price series: hard to compare at difference levels
- Simple solution: normalize price series to start at 100
- Divide all prices by first in series, multiply by 100
- Same starting point
- All prices relative to starting point
- Difference to starting point in percentage points
prices = pd.read_csv('./dataset/asset_classes.csv', parse_dates=['DATE'], index_col='DATE')
# Inspect prices here
print(prices.info())
# Slect first prices
first_prices = prices.iloc[0]
# Create normalized
normalized = prices.div(first_prices) * 100
# Plot normalized
normalized.plot();
Comparing stock prices with a benchmark
You also learned in the video how to compare the performance of various stocks against a benchmark. Now you'll learn more about the stock market by comparing the three largest stocks on the NYSE to the Dow Jones Industrial Average, which contains the 30 largest US companies.
The three largest companies on the NYSE are:
| Company | Stock Ticker |
|---|---|
| Johnson & Johnson | JNJ |
| Exxon Mobil | XOM |
| JP Morgan Chase | JPM |
stocks = pd.read_csv('./dataset/nyse.csv', parse_dates=['date'], index_col='date')
dow_jones = pd.read_csv('./dataset/dow_jones.csv', parse_dates=['date'], index_col='date')
# Concatenate data and inspect result here
data = pd.concat([stocks, dow_jones], axis=1)
print(data.info())
# Normalize and plot your data here
first_value = data.iloc[0]
normalized = data.div(first_value).mul(100).plot();
tickers = ['MSFT', 'AAPL']
# Import stock data here
stocks = pd.read_csv('./dataset/msft_aapl.csv', parse_dates=['date'], index_col='date')
# Import index here
sp500 = pd.read_csv('./dataset/sp500.csv', parse_dates=['date'], index_col='date')
# Concatenate stocks and index here
data = pd.concat([stocks, sp500], axis=1).dropna()
# Normalize data
normalized = data.div(data.iloc[0]).mul(100)
# Subtract the normalized index from the normalized stock prices, and plot the result
normalized[tickers].sub(normalized['SP500'], axis=0).plot();
Convert monthly to weekly data
You have learned in the video how to use .reindex() to conform an existing time series to a DateTimeIndex at a different frequency.
Let's practice this method by creating monthly data and then converting this data to weekly frequency while applying various fill logic options.
start = '2016-1-1'
end = '2016-2-29'
# Create monthly_dates here
monthly_dates = pd.date_range(start=start, end=end, freq='M')
# Create and print monthly here
monthly = pd.Series(data=[1, 2], index=monthly_dates)
print(monthly)
# Create weekly_dates here
weekly_dates = pd.date_range(start=start, end=end, freq='W')
# Print monthly, reindexed using weekly_dates
print(monthly.reindex(weekly_dates))
print(monthly.reindex(weekly_dates, method='bfill'))
print(monthly.reindex(weekly_dates, method='ffill'))
Create weekly from monthly unemployment data
The civilian US unemployment rate is reported monthly. You may need more frequent data, but that's no problem because you just learned how to upsample a time series.
You'll work with the time series data for the last 20 years, and apply a few options to fill in missing values before plotting the weekly series.
data = pd.read_csv('./dataset/unrate_2000.csv', parse_dates=['date'], index_col='date')
# Show first five rows of weekly series
print(data.asfreq('W').head(5))
# Show first five rows of weekly seres with bfill option
print(data.asfreq('W', method='bfill').head(5))
# Create weekly series with ffill option and show first five rows
weekly_ffill = data.asfreq('W', method='ffill')
print(weekly_ffill.head(5))
# Plot weekly_fill starting 2015 here
weekly_ffill.loc['2015':].plot()
Use interpolation to create weekly employment data
You have recently used the civilian US unemployment rate, and converted it from monthly to weekly frequency using simple forward or backfill methods.
Compare your previous approach to the new .interpolate() method that you learned about in this video.
unrate = pd.read_csv('./dataset/unrate.csv', parse_dates=['DATE'], index_col='DATE')
monthly = unrate.resample('MS').first()
monthly.head()
print(monthly.info())
# Create weekly dates
weekly_dates = pd.date_range(start=monthly.index.min(), end=monthly.index.max(), freq='W')
# Reindex monthly to weekly data
weekly = monthly.reindex(weekly_dates)
# Create ffill and interpolated columns
weekly['ffill'] = weekly.UNRATE.ffill()
weekly['interpolated'] = weekly.UNRATE.interpolate()
# Plot weekly
weekly.plot();
plt.savefig('../images/interpolate.png')
data = pd.read_csv('./dataset/debt_unemployment.csv', parse_dates=['date'], index_col='date')
print(data.info())
# Interpolate and inspect here
interpolated = data.interpolate()
print(interpolated.info())
# Plot interpolated data here
interpolated.plot(secondary_y='Unemployment');
Compare weekly, monthly and annual ozone trends for NYC & LA
You have seen in the video how to downsample and aggregate time series on air quality.
First, you'll apply this new skill to ozone data for both NYC and LA since 2000 to compare the air quality trend at weekly, monthly and annual frequencies and explore how different resampling periods impact the visualization.
ozone = pd.read_csv('./dataset/ozone_nyla.csv', parse_dates=['date'], index_col='date')
print(ozone.info())
# Calculate and plot the weekly average ozone trend
ozone.resample('W').mean().plot();
# Calculate and plot the monthly average ozone trend
ozone.resample('M').mean().plot();
# Calculate and plot the annual average ozone trend
ozone.resample('A').mean().plot();
stocks = pd.read_csv('./dataset/goog_fb.csv', parse_dates=['date'], index_col='date')
print(stocks.info())
# Calculate and plot the monthly average
monthly_average = stocks.resample('M').mean()
monthly_average.plot(subplots=True);
Compare quarterly GDP growth rate and stock returns
With your new skill to downsample and aggregate time series, you can compare higher-frequency stock price series to lower-frequency economic time series.
As a first example, let's compare the quarterly GDP growth rate to the quarterly rate of return on the (resampled) Dow Jones Industrial index of 30 large US stocks.
GDP growth is reported at the beginning of each quarter for the previous quarter. To calculate matching stock returns, you'll resample the stock index to quarter start frequency using the alias 'QS'``, and aggregating using the.first()``` observations.
gdp_growth = pd.read_csv('./dataset/gdp_growth.csv', parse_dates=['date'], index_col='date')
print(gdp_growth.info())
# Import and inspect djia here
djia = pd.read_csv('./dataset/djia.csv', parse_dates=['date'], index_col='date')
print(djia.info())
# Calculate djia quarterly returns here
djia_quarterly = djia.resample('QS').first()
djia_quarterly_return = djia_quarterly.pct_change().mul(100)
# Concatenate, rename and plot djia_quarterly_return and gdp_growth here
data = pd.concat([gdp_growth, djia_quarterly_return], axis=1)
data.columns = ['gdp', 'djia']
data.plot();
sp500 = pd.read_csv('./dataset/sp500.csv', parse_dates=['date'], index_col='date')
print(sp500.info())
# Calculate daily returns here
daily_returns = sp500.squeeze().pct_change()
# Resample and calculate statistics
stats = daily_returns.resample('M').agg(['mean', 'median', 'std'])
# Plot stats here
stats.plot()