The Best of the Best Models
In this chapter, you will become a modeler of discerning taste. You'll learn how to identify promising model orders from the data itself, then, once the most promising models have been trained, you'll learn how to choose the best model from this fitted selection. You'll also learn a great framework for structuring your time series projects. This is the Summary of lecture "ARIMA Models in Python", via datacamp.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['figure.figsize'] = (10, 5)
plt.style.use('fivethirtyeight')
Intro to ACF and PACF
- ACF : AutoCorrelation Function \
: Correlation between time series and the same time series offset by n-step
- lag-1 autocorrelation -> $corr(y_t, y_{t-1})$
- lag-2 autocorrelation -> $corr(y_t, y_{t-2})$
- $\dots$
- lag-n autocorrelation -> $corr(y_t, y_{t-n})$
- If ACF values are small and lie inside the blue shaded region, then they are not statistically significant.
- PACF : Partial AutoCorrelation Function \ : Correlation between time series and lagged version of itself after we subtract the effect of correlation at smaller lags.
- Using ACF and PACF to choose model order
| AR(p) | MA(q) | ARMA(p, q) | |
|---|---|---|---|
| ACF | Tails off | Cuts off after lag q | Tails off |
| PACF | Cuts off after lag p | Tails off | Tails off |
df = pd.read_csv('./dataset/sample2.csv', index_col=0, parse_dates=True)
df = df.asfreq('D')
df.head()
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# Create figure
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12,8))
# Plot the ACF of df
plot_acf(df, lags=10, zero=False, ax=ax1);
# Plot the PACF of df
plot_pacf(df, lags=10, zero=False, ax=ax2);
Based on the ACF and PACF plots, This is MA(3) model.
earthquake = pd.read_csv('./dataset/earthquakes.csv', index_col='date', parse_dates=True)
earthquake.drop(['Year'], axis=1, inplace=True)
earthquake = earthquake.asfreq('AS-JAN')
earthquake.head()
from statsmodels.tsa.statespace.sarimax import SARIMAX
# Create figure
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 8))
# Plot ACF and PACF
plot_acf(earthquake, lags=15, zero=False, ax=ax1);
plot_pacf(earthquake, lags=15, zero=False, ax=ax2);
Based on the ACF and PACF plots, This is AR(1) model.
model = SARIMAX(earthquake, order=(1, 0, 0))
# Train model
results = model.fit()
Intro to AIC and BIC
- AIC (Akaike Information Criterion)
- Lower AIC indicates a better model
- AIC likes to choose simple models with lower order
- BIC (Bayesian Information Criterion)
- Very similar to AIC
- Lower BIC indicates a better model
- BIC likes to choose simple models with lower order
- AIC vs BIC
- The difference between two metrics is how much they penalize model complexity
- BIC favors simpler models than AIC
- AIC is better at choosing predictive models
- BIC is better at choosing good explanatory model
df = pd.read_csv('./dataset/sample2.csv', index_col=0, parse_dates=True)
df = df.asfreq('D')
# Create figure
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12,8))
# Plot the ACF of df
plot_acf(df, lags=10, zero=False, ax=ax1);
# Plot the PACF of df
plot_pacf(df, lags=10, zero=False, ax=ax2);
order_aic_bic = []
# Loop over p values from 0-2
for p in range(3):
# Loop over q values from 0-2
for q in range(3):
# Create and fit ARMA(p, q) model
model = SARIMAX(df, order=(p, 0, q))
results = model.fit()
# Append order and results tuple
order_aic_bic.append((p, q, results.aic, results.bic))
order_df = pd.DataFrame(order_aic_bic, columns=['p', 'q', 'AIC', 'BIC'])
# Print order_df in order of increasing AIC
print(order_df.sort_values('AIC'))
# Print order_df in order of increasing BIC
print(order_df.sort_values('BIC'))
Based on this result, ARMA(2,2) model is the best fit
for p in range(3):
for q in range(3):
try:
# Create and fit ARMA(p, q) model
model = SARIMAX(earthquake, order=(p, 0, q))
results = model.fit()
# Print order and results
print(p, q, results.aic, results.bic)
except:
print(p, q, None, None)
Mean absolute error
Obviously, before you use the model to predict, you want to know how accurate your predictions are. The mean absolute error (MAE) is a good statistic for this. It is the mean difference between your predictions and the true values.
In this exercise you will calculate the MAE for an ARMA(1,1) model fit to the earthquakes time series
model = SARIMAX(earthquake, order=(1, 0, 1))
results = model.fit()
# Calculate the mean absolute error from residuals
mae = np.mean(np.abs(results.resid))
# Print mean absolute error
print(mae)
# Make plot of time series for comparison
earthquake.plot();
Diagnostic summary statistics
It is important to know when you need to go back to the drawing board in model design. In this exercise you will use the residual test statistics in the results summary to decide whether a model is a good fit to a time series.
Here is a reminder of the tests in the model summary:
| Test | Null hypothesis | P-value |
|---|---|---|
| Ljung-Box | There are no correlations in the residual | Prob(Q) |
| Jarque-Bera | The residuals are normally distributed | Prob(JB) |
model1 = SARIMAX(df, order=(3, 0, 1))
results1 = model1.fit()
# Print summary
print(results1.summary())
model2 = SARIMAX(df, order=(2, 0, 0))
results2 = model2.fit()
# Print summary
print(results2.summary())
Plot diagnostics
It is important to know when you need to go back to the drawing board in model design. In this exercise you will use 4 common plots to decide whether a model is a good fit to some data.
Here is a reminder of what you would like to see in each of the plots for a model that fits well:
| Test | Good fit |
|---|---|
| Standardized residual | There are no obvious patterns in the residuals |
| Histogram plus kde estimate | The KDE curve should be very similar to the normal distribution |
| Normal Q-Q | Most of the data points should lie on the straight line |
| Correlogram | 95% of correlations for lag greater than one should not be significant |
model = SARIMAX(df, order=(1, 1, 1))
results=model.fit()
# Create the 4 diagostics plots
results.plot_diagnostics(figsize=(20, 10));
plt.tight_layout();
plt.savefig('../images/plot_diagnostics.png')
Box-Jenkins method
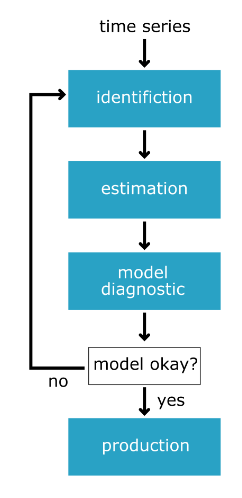
- From raw data -> production model
- identification
- estimation
- model diagnostics
- Identification
- Is the time series stationary?
- What differencing will make it stationary?
- What transforms will make it stationary?
- What values of p and q are most promising?
- Estimation
- Use the data to train the model coefficient
- Done for us using
model.fit() - Choose between models using AIC and BIC
- Model Diagnostics
- Are the residuals uncorrelated
- Are residuals normally distributed
Identification
In the following exercises you will apply to the Box-Jenkins methodology to go from an unknown dataset to a model which is ready to make forecasts.
You will be using a new time series. This is the personal savings as % of disposable income 1955-1979 in the US.
The first step of the Box-Jenkins methodology is Identification. In this exercise you will use the tools at your disposal to test whether this new time series is stationary.
savings = pd.read_csv('./dataset/savings.csv', parse_dates=True, index_col='date')
savings = savings.asfreq('QS')
savings.head()
from statsmodels.tsa.stattools import adfuller
# Plot time series
savings.plot();
# Run Dicky-Fuller test
result = adfuller(savings['savings'])
# Print test statistics
print(result[0])
# Print p-value
print(result[1])
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 8))
# Plot the ACF of savings on ax1
plot_acf(savings, lags=10, zero=False, ax=ax1);
# Plot the PACF of savings on ax2
plot_pacf(savings, lags=10, zero=False, ax=ax2);
The ACF and the PACF are a little inconclusive for this ones. The ACF tails off nicely but the PACF might be tailing off or it might be dropping off. So it could be an ARMA(p,q) model or a AR(p) model.
for p in range(4):
# Loop over q values from 0-3
for q in range(4):
try:
# Create and fit ARMA(p, q) model
model = SARIMAX(savings, order=(p, 0, q), trend='c')
results = model.fit()
# Print p, q, AIC, BIC
print(p, q, results.aic, results.bic)
except:
print(p, q, None, None)
You didn't store and sort your results this time. But the AIC and BIC both picked the ARMA(1,2) model as the best and the AR(3) model as the second best.
Diagnostics
You have arrived at the model diagnostic stage. So far you have found that the initial time series was stationary, but may have one outlying point. You identified promising model orders using the ACF and PACF and confirmed these insights by training a lot of models and using the AIC and BIC.
You found that the ARMA(1,2) model was the best fit to our data and now you want to check over the predictions it makes before you would move it into production.
model = SARIMAX(savings, order=(1, 0, 2), trend='c')
results = model.fit()
# Create the 4 diagnostics plots
results.plot_diagnostics(figsize=(20, 15));
plt.tight_layout()
# Print summary
print(results.summary())
The JB p-value is zero, which means you should reject the null hypothesis that the residuals are normally distributed. However, the histogram and Q-Q plots show that the residuals look normal. This time the JB value was thrown off by the one outlying point in the time series. In this case, you could go back and apply some transformation to remove this outlier or you probably just continue to the production stage.