Set Size

The number of elements in a set $S$ is called its size or cardinality, and denoted $\vert S \vert$ or $\# S$.

For example,

Bits: $\vert\{0, 1\}\vert = 2$
Coin: $\vert\{\text{heads, tails}\} \vert = 2$
Die: $\vert\{1, 2, 3, 4, 5, 6\}\vert = 6$
Digits: $\vert\{0, 1, \dots, 9\}\vert = 10$
Letters: $\vert \{ a, \dots, z\} \vert = 26$
Empty set: $\vert \emptyset \vert = 1$
Integers: $\vert \mathbb{Z}\vert = \vert \mathbb{N} \vert = \vert \mathbb{P} \vert = \infty$ (Countably infinite $\aleph_0$)
Reals: $\vert \mathbb{R} \vert = \infty$ (Uncountably infinite $\aleph$)

Integer Intervals

if $m \leq n, \{m, \dots n\} = \{\text{integers from m to n, inclusive}\}$,

$$ \vert \{m, \dots, n\} \vert = n - m +1 $$

Integer Multiples

$$ {}_d (n] = \{1 \leq i \leq n : d / i \} $$

For example,

${}_3(8] = \{3, 6\} = \{1\cdot3, 2\cdot3\}$
${}_3(9] = \{3, 6, 9\} = \{1\cdot3, 2\cdot3, 3\cdot3\}$

$$ \vert {}_d (n] \vert = \lfloor n/d \rfloor$$

For example,

$\vert {}_3(8] \vert = \lfloor 8/3 \rfloor = 2$
$\vert {}_3(9] \vert = \lfloor 9/3 \rfloor = 3$

Set size in Python

print(len({-1, 1}))

2

print(sum({-1, 1}))

0

print(min({-1, 1}))

-1

print(max({-1, 1}))

1

A = {1, 2, 3}
print(sum(A))

total = 0
for i in A:
    total += i
print(total)

6
6

Disjoint Unions

A union of disjoint sets is called a disjoint union.

For example,

$\{0\} \cup \{1\} = \{0, 1\}$

For disjoint sets, the size of the union is the sum of the sizes.

$$ \vert A \cup B \vert = \vert A \vert + \vert B \vert $$

Note: In set theory, it is called addition rule

Complements

Quintessential disjoint sets ($A$ and $A^{c}$) $$ A \cup A^c = \Omega \\ \vert \Omega \vert = \vert A \cup A^c \vert = \vert A \vert + \vert A^c \vert \\ \vert A^c \vert = \vert \Omega \vert - \vert A \vert $$
Note: In set theory, it is called subtraction(or complement) rule

General Subtraction Rule

$$ \begin{aligned} A \subseteq B \quad \rightarrow B &= A \cup (B - A) \\ \vert B \vert &= \vert A \vert + \vert B - A \vert \\ \vert B - A \vert &= \vert B \vert - \vert A \vert \end{aligned}$$

General Unions

Disjoint $A$ and $B$: $\vert A \cup B \vert = \vert A \vert + \vert B \vert$
Size of union = sum of sizes
In general: $\vert A \cup B \vert \neq \vert A \vert + \vert B \vert$
- $\vert \{a\} \cup \{a\} \vert = \vert \{a\} \vert = 1$
- $\vert \{ a \} \vert + \vert \{ a \} \vert = 2$

$$ \vert A \cup B \vert = \vert A \vert + \vert B \vert - \vert A \cap B \vert $$

This is Principle of Inclusion-Exclusion(or PIE for short)

Multiple sets

Two sets

$$ \vert A \cup B \vert = \vert A \vert + \vert B \vert - \vert A \cap B \vert $$

Three sets

$$ \begin{aligned} \vert A \cup B \cup C \vert &= \vert A \vert + \vert B \vert + \vert C \vert \\ &- \vert A \cap B \vert - \vert A \cap C \vert - \vert B \cap C \vert \\ &+ \vert A \cap B \cap C \vert \end{aligned}$$

n sets

$$ \Big \vert \cup_{i=1}^n A_i \Big \vert = \sum_{i \leq i \leq n} \vert A_i \vert - \sum_{1 \leq i < j \leq n} \vert A_i \cap A_j \vert + \cdots + (-1)^{n-1} \Big \vert \cap_{i=1}^n A_i \Big \vert $$

Sanity checks

$A$, $B$ disjoint

$$ \vert A \cup B \vert = \vert A \vert + \vert B \vert - \vert A \cap B \vert = \vert A \vert + \vert B \vert $$

Equal sets

$$ \vert A \cup A \vert = \vert A \vert + \vert A \vert - \vert A \cap A \vert = \vert A \vert $$

nested/disjoint

$$ \max \{ \vert A \vert, \vert B \vert \} \leq \vert A \cup B \vert \leq \vert A \vert + \vert B \vert $$

Cartesian Products

If $\vert \{a, b\} \vert = 2$ and $\vert \{1, 2, 3\} = 3$, then

$$ \{a, b\} \times \{1, 2, 3\} = \begin{Bmatrix} (a, 1) & (a, 2) & (a, 3) \\ (b, 1) & (b, 2) & (b, 3) \end{Bmatrix} $$

And,

$$ \vert \{a, b\} \times \{1, 2, 3\} \vert = 2 \times 3 = 6 $$

In general, the size of a Cartesian Product is the product of the set sizes.

$$ \vert A \times B \vert = \vert A \vert \times \vert B \vert $$

Note: In set theory, it is called Product Rule

Three Sets

If we have two sets, ($A \times B \quad \{(a, b): a \in A, b \in B \}$), its shape has rectangle, And set size is $\vert A \times B \vert = \vert A \vert \times \vert B \vert$

If we have three sets, ($A \times B \times C \quad \{(a, b, c): a \in A, b \in B c \in C\}$), then its shape has cuboid, and number of element will be

$$ \vert A \times B \times C \vert = \vert A \vert \times \vert B \vert \times \vert C \vert $$

n Sets

For $n$ sets, by Product Rule and induction,

$$ \vert A_1 \times \dots \times A_n \vert = \vert A_1 \vert \times \dots \times \vert A_n \vert $$

Cartesian Powers

Cartesian Powers of a Set

Cartesian product of a set with ifself is a Cartesian Power

Cartesian Square: $A^2 = A \times A$
$n$-th Cartesian Power: $A^n \stackrel{\text{def}}{=} \underbrace{A \times A \times \dots A}_n $
- $\vert A^n \vert = \vert A \times A \times \dots \times A \vert = \vert A \vert \times \vert A \vert \times \dots \times \vert A \vert $

Binary Strings

$ \{0, 1\}^n = \{\text{length-n binary strings}\} \quad \text{or n-bit strings}$
$\vert \{0, 1\}^n \vert = \vert \{0, 1\} \vert^n = 2^n $

Subsets

The power set of $S$, denoted $\mathbb{P}(S)$ is the collection of all subsets of $S$,

$$ \mathbb{P}(\{a, b\}) = \Big\{ \{ \}, \{a\}, \{b\}, \{a,b\}\Big\} $$

By the 1-1 correspondence betwen $\mathbb{P}(S)$ and $\{0,1\}^{\vert S \vert}$,

$$ \vert \mathbb{P}(S) \vert = \vert \{0, 1\}^{\vert S \vert} \vert = 2^{\vert S \vert} $$

The size of the power set is the power of the set size.

Functions

A function from $A$ to $B$ maps every element $a \in A$ to an element $f(a) \in B$

Define a function $f$: specify $f(a)$ for every $a \in A$
- $f$ from $\{1, 2, 3\}$ to $\{p, u\}$: $f(1)=p, f(2)=u, f(3)=p$
- $f: 3-\text{tuple}(f(1), f(2), f(3)): (p, u, p)$
- $\{\text{functions from } \{1, 2, 3\} \text{ to } \{p, u\}: \{p, u\} \times \{p, u\} \times \{p, u\}$
- size of functions from $\{1, 2, 3\}$ to $\{p, u\}$ = $2^3 = \vert \{p, u\} \vert^{\vert \{1, 2, 3\} \vert}$
$\{\text{functions from } A \text{ to } B \} \quad \underbrace{B \times B \times \dots \times B}_{\vert A \vert} = B^{\vert A \vert}$
- Size of functions from $A$ to $B$: $\vert B^{\vert A \vert} \vert = \vert B \vert^{\vert A \vert}$

Cartesian Powers in Python

Cartesian Power

import itertools

print(set(itertools.product({2, 5, 9}, repeat=2)))

{(5, 9), (5, 5), (2, 9), (9, 2), (9, 9), (2, 2), (9, 5), (2, 5), (5, 2)}

Exponent

3 ** 2

9

Counting Variations

PIN

PIN is short for Personal Identification Number. What if we have 4-digits PIN, how many variation of each PIN?

$$ D = \{0, \dots, 9\} \\ \{\text{4-digit PIN}\} = D^4 \\ \vert D^4 \vert = \vert D \vert^4 = 10^4$$

Variable Length

Consider 3-5 digit PINs.

$$ D = \{0, \dots, 9\}, \{\text{PINs}\} = D^3 \cup D^4 \cup D^5 $$

In this case,

$$ \sharp \text{ of PINs} = \vert D^3 \cup D^4 \cup D^5 \vert = \vert D^3 \vert + \vert D^4 \vert + \vert D^5 \vert = 10^3 + 10^4 + 10^5 $$

PINs Containing Zero

Consider 4 digit PINs with containing zero

$D = \{0, 1, \dots, 9\}$
$Z = \{0\}, \bar{Z} = \{1, 2, \dots, 9\}$
Note: $\bar{Z} = Z^c$: set of non-zero digits
$x^n \triangleq x_1, \dots, x_n$ - ($n$-digit sequence)

$\qquad \rightarrow \exists Z = \{ x^n \in D^n : \exists i x_i \in Z\} $: {$n$-digit PINs containing 0}

$\vert \exists Z \vert = ?$

2-Digit case - Inclusion-Exclusion

$$ \exists Z = \{x_1 x_2 : \exists i \quad x_i = 0\} $$

$Z_1 = \{x_1 x_2: x_1 = 0\}$
$Z_2 = \{x_1 x_2: x_2 = 0\}$
$\exists Z = Z_1 \cup Z_2$
$\vert \exists Z \vert = \vert Z_1 \vert + \vert Z_2 \vert - \vert Z_1 \cap Z_2 \vert $

2-Digit case - Complement Rule

$$ \exists Z = \{x_1 x_2 : \exists i \quad x_i = 0\} $$

$\omega = D^2$
$\bar{\exists Z} = \bar{\{x_1 x_2: \exists i \quad x_i = 0 \}} = \{x_1 x_2: \forall i \quad x_i \neq 0\} = \bar{Z} \times \bar{Z}$
$ \vert \bar{ \exists Z} \vert = \vert \bar{Z} \times \bar{Z} \vert = \vert \bar{Z} \vert^2 $

n-Digit case - Inclusion-Exclusion

$$ \exists Z = \{ x^n : \exists i \quad x_i = 0 \} $$

$Z_i = \{x^n: x_i = 0\}$
$\exists Z = Z_1 \cup \dots \cup Z_n$
$\vert \exists Z \vert = \vert Z_1 \vert + \vert Z_2 \vert + \dots + \vert Z_n \vert - \vert Z_1 \cap Z_2 \vert - \vert Z_1 \cap Z_3 \vert - \dots - \vert Z_{n-1} \cap Z_n \vert \\ + (-1)^{n-1} \vert Z_1 \cap Z_2 \cap \dots \cap Z_n \vert$

n-Digit case - Complement Rule

$$ \bar{\exists Z} = \bar{\{x^n \vert \exists i \quad x_i \in Z\}} = \{x^n \vert \forall i \quad x_i \not \in Z \} = (\bar{Z})^n \triangleq \forall \bar{Z} $$

$\vert \forall \bar{Z} \vert = \vert \bar{Z} \vert^n = 9^n$
$\exists Z = D^n - \forall \bar{Z} $
$\vert \exists Z \vert = \vert D^n \vert - \vert \forall \bar{Z} \vert = 10^n - 9^n$

Counting Trees

Why Trees

A tree can represent any set of sequence, not just Cartesian Products
And it enables systematic counting technique
And it is useful in model random phenomena

Exercise 1

Exercise 1.1

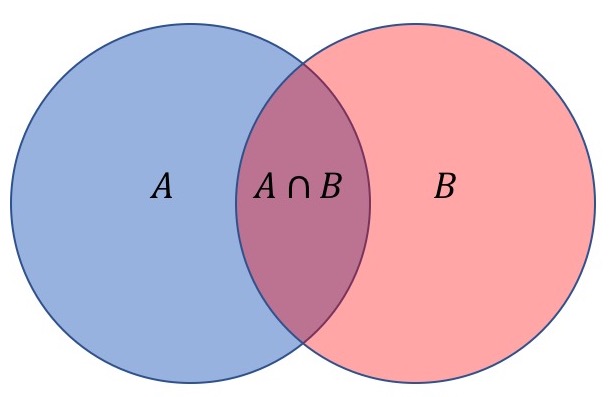
The inclusion-exclusion principle states that for two sets $A$ and $B$,

$$|A\cup B|=|A|+|B|-|A\cap B|.$$

Write the following functions to determine $|A\cup B|$ in two different ways.

A function union that determines first $A\cup B$ and then evaluates the union's size. Output the ordered pair $(A\cup B, |A\cup B|)$.

* **Sample run** *

A = {1, 2, 3}
B = {3, -6, 2, 0}
print union(A, B)

* **Expected Output** *

({-6, 0, 1, 2, 3}, 5)

def union(A, B):
    # inputs: A and B are of type 'set'
    # output: a tuple of the type (set, set_length)
    union_set = A.union(B)
    union_size = len(union_set)
    return (union_set, union_size)

A = {1,4,-3, "bob"}
B = {2,1,-3,"jill"}
assert union(A,B) == ({-3, 1, 2, 4, 'bob', 'jill'}, 6)

Exercise 1.2

A function inclusion_exclusion that first deterimines $|A|$, $|B|$, $A\cap B$, and $|A\cap B|$, and then uses the inclusion-exclusion formula to determine $|A\cup B|$. Output the tuple $(|A|, |B|, |A\cap B|, |A\cup B|)$.

* **Sample run:** *

A = {1, 2, 3}
B = {3, -6, 2, 0}
print inclusion_exclusion(A, B)
print "notice: 3 + 4 - 2 == 5"

* **Expected Output:** *

(3, 4, 2, 5)
notice: 3 + 4 - 2 == 5

def inclusion_exclusion(A, B):
    # inputs: A and B are of type 'set'
    # output: a tuple of four integers
    union_set = A.union(B)
    intersect_set = A.intersection(B)
    return (len(A), len(B), len(intersect_set), len(union_set))

A = {1, 2, 3, 4, 5}
B = {0, 2, -6, 5, 8, 9}
assert inclusion_exclusion(A, B) == (5, 6, 2, 9)

Exercise 2

The inclusion-exclusion principle says that for three sets $A$, $B$ and $C$,

$$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C|$$

We will write the following functions to determine $|A\cup B\cup C|$ in two different ways.

Exercise 2.1

Write function union3 that first determines $A\cup B\cup C$ and then evaluates the size of this union. Output the tuple $(A\cup B\cup C, |A\cup B\cup C|)$.

* **Sample run:** *

A = {1, 2, 3, 4, 5}
B = {0, 2, -6, 5, 8, 9}
C = {2, 10}
union3(A, B, C)

* **Expected Output:** *

({-6, 0, 1, 2, 3, 4, 5, 8, 9, 10}, 10)

def union3(A, B, C):
    # inputs: A, B and C are of type 'set'
    # output: a tuple of the type (set, set_length)
    
    union_set = A.union(B).union(C)
    return (union_set, len(union_set))

A = {1, 2, 4, 5, 10}
B = {5, 2, -6, 5, 8, 9}
C = {2, 10, 13}
assert union3(A,B,C) == ({-6, 1, 2, 4, 5, 8, 9, 10, 13}, 9)

Exercise 2.2

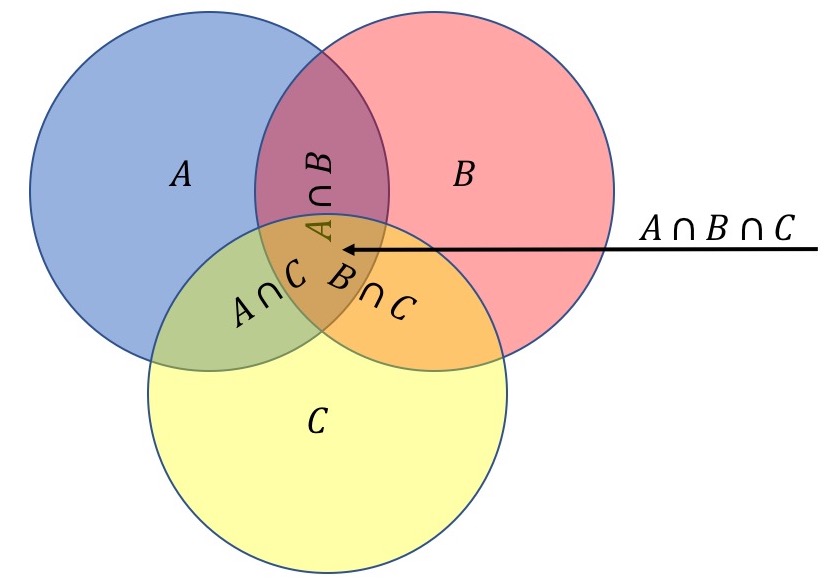
A function inclusion_exclusion3 that first deterimines the sizes of $A$, $B$, $C$ and their mutual intersections, and then uses the inclusion-exclusion principle to determine the size of the union. Output the tuple $(|A\cap B\cap C|, |A\cup B\cup C|)$. Note that for brevity we are asking you to output the intermediate answer just for $A\cap B\cap C$, but you need to calculate all.

* **Sample run:** *

A = {1, 2, 3, 4, 5}
B = {0, 2, -6, 5, 8, 9}
C = {2, 10}
print inclusion_exclusion3(A, B, C)

* **Expected Output:** *

(1, 10)

def inclusion_exclusion3(A, B, C):
    # inputs: A, B and C are of type 'set'
    # output: a tuple of two integers
    
    intersect_set = A.intersection(B).intersection(C)
    union_set = A.union(B).union(C)
    
    return (len(intersect_set), len(union_set))

A = {1, 2, 4, 5, 10}
B = {5, 2, -6, 5, 8, 9, 10}
C = {2, 10, 13}
assert inclusion_exclusion3(A,B,C) == (2, 9)