Policy Evaluation
A summary of "Understanding deep reinforcement learning"
Policy Evaluation
Policy Evalutaion
Given a MDP and a policy $\pi$, how can we measure the goodness of this policy? Policy evaluation is to find the true value function for the given policy. It uses the Bellman equation. Obtaining a true value function with the current policy is done with one step backup.
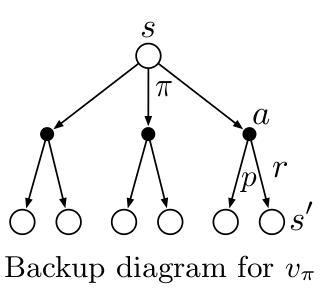
Backup means that the current values are calculated using the next values.
- One step backup vs. multi-step backup
- Full-width backup vs. sample backup (through sampling)
Policy Evaluation for MDP
The Bellman equations are simplified as follows:
(assumes in discrete state space)
Dynamic Programming
Dynamic programming is developed by Richard Bellman in the 1950s. It is kind of mathematical optimization algorithm, and it simplify a complicated problem by breaking it down into a sequence of simpler sub-problems in a recursive equation.
- Examples
- Dijkstra’s algorithm for the shortest path problem
- The Bellman-Ford algorithm for finding the shortest distance in a graph
- The Viterbi algorithm for hidden markov model (HMM)
Dynamic Programming for solving finite MDP with a policy
- Iterative Policy Evaluation
- Initialize values $V_0(s) = 0$ for all states $s$
- Repeat until convergence
- For each state $s \in S$,
This is called a Bellman (synchronous) backup for a policy $\pi$. And this recursive algorithm converges when $\gamma < 1 \text{ or } T_{ss’}^{\pi} < 1$ for all $s, s’ \in S$.
Backup Diagram for policy Evaluation